Grafy¶
Do analizy grafów stosujemy popularną bibliotekę networkx. Niniejszy kod został przygotowany z wersją 2.6.2 tego oprogramowania oraz z wersją 3.8.11 Pythona. Uwaga: wyższe wersje networkx niekoniecznie muszą być kompatybilne.
import networkx as nx # popularna biblioteka do analizy grafów
from networkx.algorithms import approximation as nalg # algorytmy na grafach
print("networkx:", nx.__version__)
!python --version
networkx: 2.6.2
Python 3.8.11
Pozostałe używane biblioteki są standardowe:
import numpy as np # numeryka
import matplotlib.pyplot as plt # grafika
import matplotlib.colors as colors
from matplotlib.patches import FancyArrowPatch, Circle
Ustawiamy domyślne parametry dla rozmiaru i rozdzielczości wykresów:
plt.rcParams["figure.figsize"] = (3,2.3) # rozmiar x i y wykresów w calach
plt.rcParams["figure.dpi"] = 120 # rozdzielczość dpi
Rozgrzewka¶
Zaczynamy od tworzenia i rysowania bardzo prostych grafów. Podstawowe definicje można znaleźć w rozdz. [5.1].
G = nx.Graph() # graf pusty
G.add_node("1") # dodanie wierzchołka "1"
# narysuj graf z parametrami grafiki
nx.draw_networkx(G,node_size=100,font_size=8,font_color='white',font_weight='bold')
plt.axis('off') # usuń ramkę
plt.show()

# dodaj więcej wierzchołków
G.add_node('A') # pojedynczy wierzchołek
G.add_nodes_from([2, 3]) # zakres wierzchołków
# dodaj krawędzie
G.add_edge(2,'A') # łączy wierzchołek 2 z 'A' itd.
G.add_edge(2, 3)
# narysuj graf z parametrami grafiki
nx.draw_networkx(G,node_size=100,font_size=8,font_color='white',font_weight='bold')
plt.axis('off')
plt.show()
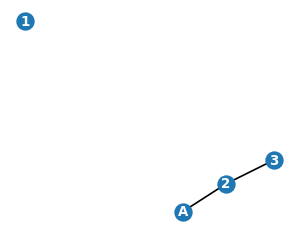
Rozłożenie wierzchołków
Jeśli wykonamy powyższą komórkę ponownie, układ wierzchołów może być inny. Wynika to stąd, że networkx ustawia je wg pewnej losowej procedury.
Dla danego grafu możemy „wyłowić” jego wierzchołki i krawędzie:
list(nx.nodes(G))
['1', 'A', 2, 3]
list(nx.edges(G))
[('A', 2), (2, 3)]
Możemy też znaleźć stopnie wierzchołków
list(nx.degree(G)) # stopnie wierzchołków
[('1', 0), ('A', 1), (2, 2), (3, 1)]
i ich histogram:
nx.degree_histogram(G) # histogram stopni wierzchołków
[1, 2, 1]
Powyższe oznacza, że w \(G\) mamy jeden wierzchołek stopnia 0 (izolowany), dwa stopnia 1 i jeden stopnia 2.
Możemy też jawnie zadać położenie wierzchołków na płaszczyżnie, co jest bardzo przydatne w rysowaniu grafów:
G=nx.Graph() # inicjalizacja - graf pusty
# zadajemy położenie i etykiety wierzchołków
G.add_node(0,pos=(0,0),label='s')
G.add_node(1,pos=(0,1),label='1')
G.add_node(2,pos=(1,0),label='2')
G.add_node(3,pos=(1,1),label='3')
# nadajemy krawędziom wagi
G.add_edge(1,2, weight="w")
G.add_edge(0,2, weight=5)
G.add_edge(1,3, weight=2)
G.add_edge(2,3, weight=1)
G.add_edge(0,1, weight=4)
# wyciągamy atrybuty grafu
pos = nx.get_node_attributes(G,'pos') # położenia wierzchołków
labels = nx.get_node_attributes(G,'label') # etykiety wierzchołków
weights = nx.get_edge_attributes(G,'weight') # wagi krawędzi
# narysuj wierzchołki
nx.draw_networkx_nodes(G,pos,node_size=100)
nx.draw_networkx_labels(G,pos,labels,font_color='white',font_weight='bold',font_size=8)
# narysuj krawędzie, tutaj etykiety utożsamiamy z wagami (edge_labels=weights)
nx.draw_networkx_edges(G,pos,width=1.5)
nx.draw_networkx_edge_labels(G,pos,edge_labels=weights,font_size=8)
plt.axis('off') # usuń ramkę
plt.show()
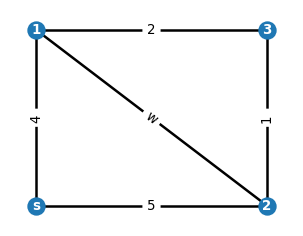
Biblioteka networkx posiada bardzo wiele funkcji działających na grafach. Poniżej ukazujemy kilka z nich.
# podgraf grafu G, zawierający wierzchołki 1,2,3
nx.draw_networkx(nx.subgraph(G,[1,2,3]),pos,labels,node_size=100,
font_color='white',font_weight='bold',font_size=8)
plt.axis('off')
plt.show()
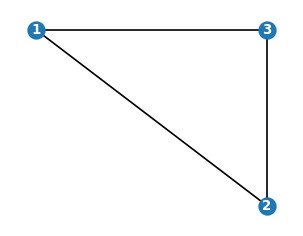
Zauważmy, że rozmieszenie wierzchołków w powyższym podgrafie jest takie samo jak w \(G\), dzięki użyciu atrybutu pos.
# uzupełnienie (do grafu pełnego)
nx.draw_networkx(nx.complement(G),pos,labels,node_size=100,
font_color='white',font_weight='bold',font_size=8)
plt.axis('off')
plt.show()
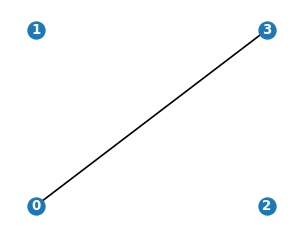
Istotnie, dodanie powyższego grafu do \(G\) uzupełnia „brakującą” krawędź i daje w wyniku graf pełny.
# konwersja grafu nieskierowanego do skierowanego
H=nx.to_directed(G)
nx.draw_networkx(H,pos,labels,node_size=100,
font_color='white',font_weight='bold',font_size=8)
plt.axis('off')
plt.show()
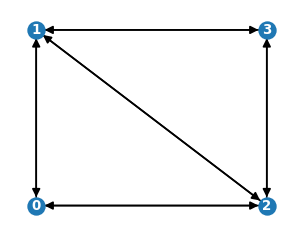
Mosty królewieckie¶
A teraz najsłynniejszy problem. Utwórzmy graf mostów królewieckich z rys. [5.5]. Ponieważ występują tu krawędzie wielokrotne, stosujemy funkcję MultiGraph.
G = nx.MultiGraph() # multigraf dla przypadku wielokrotnych krawędzi
G.add_node('A',label='A',pos=(0,-1)) # dodaj wierzchołki
G.add_node('B',label='B',pos=(0,0))
G.add_node('C',label='C',pos=(0,1))
G.add_node('D',label='D',pos=(1,0))
G.add_edge('A','B') # dodaj krawędzie
G.add_edge('B','A')
G.add_edge('C','B')
G.add_edge('B','C')
G.add_edge('A','D')
G.add_edge('B','D')
G.add_edge('C','D')
pos=nx.get_node_attributes(G,'pos')
nx.draw_networkx(G,pos,node_size=100,
font_color='white',font_weight='bold',font_size=8)
plt.axis('off')
plt.show()
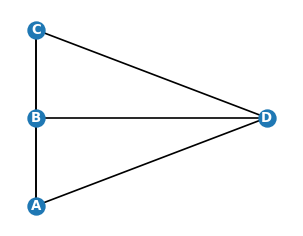
Krawędzie wielokrotne
Powyżej niestety nie widać krawędzi wielokrotnych, które się nakładają na siebie, z czym funkcja draw-networkx ma kłopoty!
Rozwiązaniem jest rysowanie krawędzi wg przepisu 3 ze strony https://www.py4u.net/discuss/22430 od użytkownika atomh33ls. Aby ten prosty przepis zrozumieć, zobaczmy najpierw, jak MultiGraph reprezentuje krawędzie:
list(G.edges)
[('A', 'B', 0),
('A', 'B', 1),
('A', 'D', 0),
('B', 'C', 0),
('B', 'C', 1),
('B', 'D', 0),
('C', 'D', 0)]
Każda krawędź jest krotką, np. (A, B, 0). Widzimy, że w przypadku krawędzi wielokrotnych są one rozróżniane elementem numer 2 krotki, który w naszym konkretnym przypadku przyjmuje wartości 0 lub 1. W szczególności, mamy dwie krawędzie od A do B: (A, B, 0) oraz (A, B, 1). Idea poniższego przepisu jest taka, by krzywizna krawędzi zależała od jej numeru.
nx.draw_networkx_nodes(G, pos, node_size = 100) # narysuj wierzchołki
labels = nx.get_node_attributes(G,'label') # etykiety wierzchołków
nx.draw_networkx_labels(G,pos,labels,font_color='white',font_weight='bold',font_size=8)
for e in G.edges: # pętla po krawędziach
plt.annotate("",
xy=pos[e[0]], xycoords='data',
xytext=pos[e[1]], textcoords='data',
arrowprops=dict(arrowstyle="-", color="black",
shrinkA=5, shrinkB=5,
patchA=None, patchB=None,
# krzywizna jest proporcjonalna do e[2]
connectionstyle="arc3,rad=rrr".replace('rrr',str(0.5*e[2])
),
),
)
plt.axis('off')
plt.show()
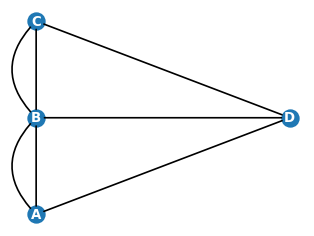
Poniżej kilka definicji z rozdz. [5.1] w zastowaniu do grafu mostów królewieckich:
list(nx.degree(G)) # stopnie wierzchołków
[('A', 3), ('B', 5), ('C', 3), ('D', 3)]
A=nx.adjacency_matrix(G) # macierz sąsiedztwa
print(A) # format dla tzw. macierzy rzadkiej
# nr wierzchołków liczba krawędzi
(0, 1) 2
(0, 3) 1
(1, 0) 2
(1, 2) 2
(1, 3) 1
(2, 1) 2
(2, 3) 1
(3, 0) 1
(3, 1) 1
(3, 2) 1
a = A.todense() # macierz sąsiedztwa w postaci zwykłej tablicy
print(a)
[[0 2 0 1]
[2 0 2 1]
[0 2 0 1]
[1 1 1 0]]
list(nx.generate_adjlist(G)) # listy incydencji
['A B B D', 'B C C D', 'C D', 'D']
Uwaga!
Widzimy, że w networkx przyjęta jest bardziej oszczędna konwencja dla list incydencji niż w książce (por. rozdz. [5.1]). Sąsiadujące wierzchołki podawane są tylko „w jedną stronę”, np. od A do B (pierwsza lista powyżej), ale wtedy nie są już podawane od B do A (druga lista), itp. Prowadzi to do bardziej zwięzłego zapisu.
nx.is_eulerian(G) # graf oczywiście nie jest eulerowski
False
Można też utworzyć graf w oparciu o listy incydencji:
K=nx.MultiGraph()
K = nx.from_numpy_matrix(a, parallel_edges = True, create_using = nx.MultiGraph())
# dodajemy jeszcze 2 krawędzie
K.add_edge(0,1)
K.add_edge(1,2)
print(list(nx.edges(K)))
[(0, 1), (0, 1), (0, 1), (0, 3), (1, 2), (1, 2), (1, 2), (1, 3), (2, 3)]
Schematy rozłożenia wierzchołków
W networkx możemy stosować rozmaite schematy rozłożenia wierzchołków. Dodatkowo, każdy schemat posiada element losowy, co prowadzi do innego rysunku przy kolejnych wywoływaniach funkcji rysującej graf.
Poniżej sprawdź różne schematy:
nx.spring_layout(G), nx.kamada_kawai_layout(G), nx.random_layout(G), nx.shell_layout(G), nx.circular_layout(G), nx.spectral_layout(G)
pos=nx.spring_layout(K) # ustawienie pozycji wierzchołków w spring_layout
nx.draw_networkx_nodes(K, pos, node_size = 100) # narysuj wierzchołki
for e in K.edges: # pętla po krawędziach, jak w poprzednim przykładzie
plt.annotate("",
xy=pos[e[0]], xycoords='data',
xytext=pos[e[1]], textcoords='data',
arrowprops=dict(arrowstyle="-", color="black",
shrinkA=5, shrinkB=5,
patchA=None, patchB=None,
connectionstyle="arc3,rad=rrr".replace('rrr',str(0.5*e[2])
),
),
)
plt.axis('off')
plt.show()
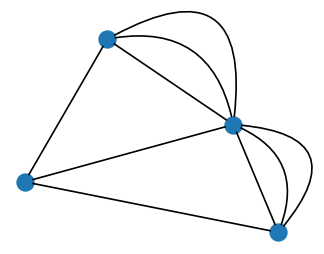
Ponieważ stopnie dokładnie dwóch wierzchołków są nieparzyste, zgodnie z wnioskami [5.1] i [5.2] graf \(K\) nie jest eulerowski, ale jest półeulerowski:
list(nx.degree(K)) # stopnie wierzchołków
[(0, 4), (1, 7), (2, 4), (3, 3)]
nx.is_eulerian(K) # graf K nie jest eulerowski
False
nx.is_semieulerian(K) # ... ale jest półeulerowski
True
A oto droga Eulera (zaczyna się w wierzchołku 3 i kończy w wierzchołku 1, gdzie obydwa są stopnia nieparzystego):
list(nx.eulerian_path(K))
[(1, 0), (0, 1), (1, 0), (0, 3), (3, 1), (1, 2), (2, 1), (1, 2), (2, 3)]
Kalejdoskop grafów¶
Bez trudu możemy wygenerować różne typowe grafy, zob. rozdz. [5.3]:
K5 = nx.complete_graph(5) # graf pełny
nx.draw_circular(K5,node_size=100)
plt.axis('equal')
plt.show()
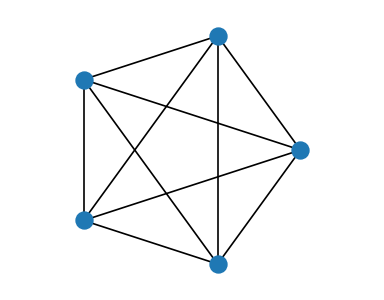
K33 = nx.complete_bipartite_graph(3,3) # graf dwudzielny pełny
# położenia wierzchołków zadane z pomocą słownika
posi = {0:[-1,1], 1:[0,1], 2:[1,1], 3:[-1,-1], 4:[0,-1], 5:[1,-1]}
nx.draw(K33,posi,node_size=100)
plt.show()
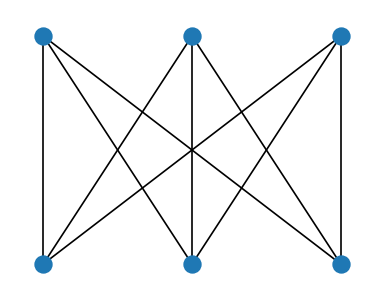
H = nx.dodecahedral_graph() # graf platoński (12-ścian foremny)
nx.draw(H,node_size=100)
plt.axis('equal')
plt.show()
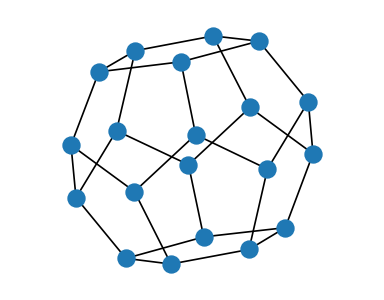
Graf \(H\) jest regularny (stopień każdego wierzchołka jest taki sam i wynosi 3):
print(list(nx.degree(H)))
[(0, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3), (7, 3), (8, 3), (9, 3), (10, 3), (11, 3), (12, 3), (13, 3), (14, 3), (15, 3), (16, 3), (17, 3), (18, 3), (19, 3)]
Badanie grafów¶
Poniższa funkcja podaje podstawowe informacje o grafie:
def graf_info(G):
st=str(type(G))
print("Liczba wierzchołków: ", int(G.number_of_nodes()))
print("Liczba krawędzi: ", int(G.number_of_edges()))
print("Lista wierzchołków: ", list(G.nodes()))
print("Lista krawędzi: ", list(G.edges()))
if "Di" not in st: # dla grafu
print("Stopnie całkowite wierzchołków: ", dict(G.degree()))
if "DiGraph" in st:
print("Stopnie wejściowe wierzchołków: ", dict(G.in_degree()))
print("Stopnie wyjściowe wierzchołków: ", dict(G.out_degree()))
Możemy badać różne typy grafów. Poniższą analizę należy powtórzyć dla wszystkich możliwości:
graf nieskierowany prosty (Graph)
graf nieskierowany z możliwymi krawędziami wielokrotnymi i pętlami (MultiGraph)
graf skierowany prosty (DiGraph)
graf skierowany z możliwymi krawędziami wielokrotnymi i pętlami (MultiDiGraph)
# sprawdź po kolei wszystkie możliwości
G=nx.Graph()
# G=nx.MultiGraph()
# G=nx.DiGraph()
# G=nx.MultiDiGraph()
Automatyczne dodawanie wierzchołków
Przy dodawaniu krawędzi, wierzchołki na ich końcach dodają się automatycznie, więc nie musimy wykonywać polecenia G.add_nodes(…)
# Tworzymy graf z wagami, nazwanymi 'dist'
G.add_weighted_edges_from([
# dodajemy krawędź między wierzchołkami 1 i 2 o wadze 7
(1, 2, 7),
# dodajemy ponownie krawędź między wierzchołkami 1 i 2, tym razem o wadze 3
# MultiGraph/MultiDiGraph ją uwzględniają, Graph/DiGraph ignorują
# rysunek ignoruje krawędzie wielokrotne
(1, 2, 3),
# dodajemy krawędź między wierzchołkami 2 i 1 o wadze 1
# MultiGraph, DiGraph, MultiDiGraph uwzględniają, Graph ignoruje
(2, 1, 1),
# dodajemy pętlę, rysunek ignoruje pętle
(6, 6, 3),
# pozostałe wierzchołki
(2, 4, 15),
(4, 5, 6),
(5, 6, 9),
(6, 1, 14),
(1, 3, 9),
(2, 3, 10),
(3, 4, 11),
(3, 6, 2),
], weight='dist')
graf_info(G)
Liczba wierzchołków: 6
Liczba krawędzi: 10
Lista wierzchołków: [1, 2, 6, 4, 5, 3]
Lista krawędzi: [(1, 2), (1, 6), (1, 3), (2, 4), (2, 3), (6, 6), (6, 5), (6, 3), (4, 5), (4, 3)]
Stopnie całkowite wierzchołków: {1: 3, 2: 3, 6: 5, 4: 3, 5: 2, 3: 4}
Jesteśmy gotowi narysować nasz graf!
nodePos = nx.spring_layout(G) # położenia wierzchołków
label_weight=nx.get_edge_attributes(G,'dist') # etykiety krawędzi
nx.draw_networkx(G, pos=nodePos, with_labels=True, font_size=8, font_color='white',
font_weight='bold',node_size=70)
# rysowanie etykiet krawędzi nie działa dla MultiGraph i MultiDiGraph
if 'Multi' not in str(type(G)):
nx.draw_networkx_edge_labels(G, pos=nodePos, edge_labels=label_weight,font_size=8);
plt.axis('off')
plt.show()
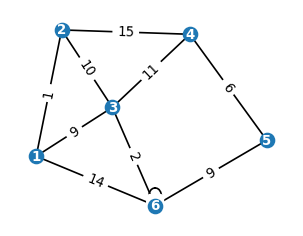
Możemy badać wiele innych cech grafu, np.
# sąsiedzi wskazanego wierzchołka
print("Lista wierzchołków osiągalnych z 1 w pojedynczym kroku:", list(G.neighbors(1)))
Lista wierzchołków osiągalnych z 1 w pojedynczym kroku: [2, 6, 3]
nx.is_biconnected(G) # dwuspójność, tj. trzeba przeciąć min 2 krawędzie, by rozspójnić
True
Algorytmy na grafach¶
Przeszukiwanie wszerz¶
W rozdz. [5.7] i [5.8] omówiono niektóre podstawowe algorytmy stosowane w analizie grafów. Poniżej podajemy „autorski” program dla algorytmu [5.3] przeszukiwania grafu wszerz. Algorytm sprawdza też „przy okazji”, czy graf jest spójny i w tym przypadku zwraca drzewo spinające grafu. Jeśli graf nie jest spójny, zwracane jest drzewo spinające części spójnej zawierającej wierzchołek startowy przeszukiwania.
def wszerz(GG,deb=False):
"""
przesukiwanie wszerz
input:
GG - graf w formacie Graph
deb - boolean, kontrola wydruku
output:
jeśli GG spójny - drzewo spinające
jeśli GG niespójny - drzewo spinające części spójnej zawierającej wierzchołek startowy
"""
G=GG.copy() # kopia grafu (będzie "psuta")
T=nx.Graph() # zainicjalizuj puste drzewo spinające
V=list(nx.nodes(G)) # lista wierzchołków nieodwiedzonych
V2=[] # pusta lista wierzchołków odwiedzonych
V2.append(V.pop(0)) # przenieś wierzchołek 0 z nieodwiedzonych do odwiedzonych
if len(V) == 0: # specjalny przypadek, gdy G ma tylko jeden wierzchołek
if deb:
print('jeden wierzchołek')
T.add_nodes_from(V2)
return T
lv=len(V) # obecna liczba wierzchołków nieodwiedzonych
lv2=lv+1 # cokolwiek innego od lv, by poniższa pętla ruszyła
while len(V)>0 and lv != lv2: # wykonuj, dopóki są wierzchołki nieodwiedzone
# i ich liczba się zmienia, tj. lv != lv2
lv=lv2 # obecna liczba wierzchołków lv nieodwiedzonych = poprzedniej
VV2=V2.copy() # skopiuj listę nieodwiedzonych
for v2 in VV2: # pętla po wierzchołkach odwiedzonych
VV=V.copy() # skopiuj listę nieodwiedzonych
for v in VV: # pętla po wierzchołkach nieodwiedzonych
if (v2, v) in G.edges(): # jeśli odwiedzony i nieodwiedzony sąsiadują
V.remove(v) # przenieś wierzchołek z nieodwiedzonych
V2.append(v) # do odwiedzonych
G.remove_edge(v2,v) # usuń krawędź z grafu
T.add_edge(v2,v) # i dodaj ją do drzewa
lv2=lv-1 # liczba nieodwiedzonych zmniejsza się o 1
# To się wykona, jeśli graf jest niespójny. Wówczas lv się nie zmienia, a istnieją nieodwiedzone!
if len(V)>0:
if deb:
print('niespójny!')
return T
Test algorytmu na przykładowym grafie:
G = nx.Graph()
# G.add_nodes_from([0])
G.add_nodes_from([0,1,2,3,4,5,6,7,8,9,'A','B','C','r'])
G.add_edges_from([(0,0),(1,3),(3,1),(5,0),(5,'A'),
(2,3),(4,3),(2,4),(7,4),(7,4),(6,9),(5,8),(0,1),(0,9),(0,9),(1,9),('B','C'),(7,8)])
H=G.copy()
T=wszerz(H,True)
niespójny!
plt.figure(figsize=(3,3))
nodePos = nx.spring_layout(H)
nx.draw_networkx(H, pos=nodePos, with_labels=True,
node_size=60,font_color='white',font_size=8)
nx.draw_networkx_edges(T, pos=nodePos,edge_color='r',width=3)
plt.axis('equal')
plt.axis('off')
plt.show()
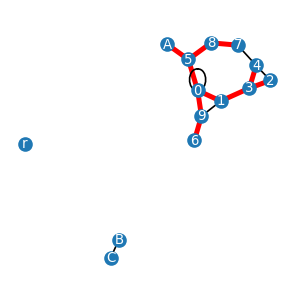
Widzimy uzyskane drzewo spinające, oznaczone na czerowno, dla składowej spójnej grafu zawierajacej wierzchołek startowy 0.
Możemy teraz łatwo utworzyć funcję sprawdzającą ile spójnych składowych ma graf.
def ile_skl(GG):
G=GG.copy() # skopiuj graf, bo będzie się zmieniać
i=0 # początkowa liczba składowych grafu
while nx.number_of_nodes(G)>0: # wykonuj, dopóki G jest niepusty
T=wszerz(G)
G.remove_nodes_from(T) # usuń uzyskane drzewo z grafu
i=i+1 # liczba składowych wzrasta o 1
print('liczba składowych spójnych:',i)
return i # ostateczna liczba składowych
ile_skl(G)
liczba składowych spójnych: 3
3
Podobnie, możemy uzyskać las drzew spinających, sumując drzewa spinające poszczególnych składowych spójnych grafu:
def las(GG):
G=GG.copy() # skopiuj graf, bo będzie się zmieniać
L=nx.Graph() # las
i=0 # początkowa liczba składowych grafu
while nx.number_of_nodes(G)>0: # wykonuj, dopóki G jest niepusty
T=wszerz(G)
G.remove_nodes_from(T) # usuń uzyskane drzewo z grafu
L=nx.union(L,T) # dodaj drzewo T do lasu L
i=i+1 # liczba składowych wzrasta o 1
print('liczba składowych spójnych:',i)
return L # las spinający
lasek=las(G)
graf_info(lasek)
liczba składowych spójnych: 3
Liczba wierzchołków: 14
Liczba krawędzi: 11
Lista wierzchołków: [0, 1, 5, 9, 3, 8, 'A', 6, 2, 4, 7, 'B', 'C', 'r']
Lista krawędzi: [(0, 1), (0, 5), (0, 9), (1, 3), (5, 8), (5, 'A'), (9, 6), (3, 2), (3, 4), (8, 7), ('B', 'C')]
Stopnie całkowite wierzchołków: {0: 3, 1: 2, 5: 3, 9: 2, 3: 3, 8: 2, 'A': 1, 6: 1, 2: 1, 4: 1, 7: 1, 'B': 1, 'C': 1, 'r': 0}
plt.figure(figsize=(3, 3))
nodePos = nx.spring_layout(G)
nx.draw_networkx(G, pos=nodePos, with_labels=True,
node_size=50,font_color='white',font_size=8)
nx.draw_networkx_edges(lasek, pos=nodePos,edge_color='r',width=3)
plt.axis('equal')
plt.axis('off')
plt.show()
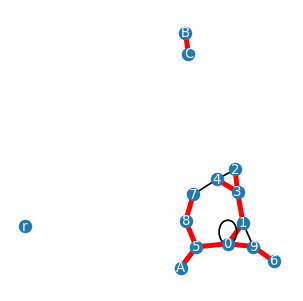
Algorytmy wbudowane w networkx¶
Algorytmy networkx
Biblioteka networkx zawiera wiele bardzo użytecznych algorytmów działających na grafach. Są one „profesjonalne” i należy ich używać, gdy tylko możliwe. Powyższy algorytm „autorski” miał na celu pokazanie, że algorytmy na grafach i implementujące je programy są w swojej istocie proste i łatwe w zrozumieniu.
Utwórzmy przykładowy graf skierowany i przeszukajmy go w głąb i wszerz:
G = nx.DiGraph()
G.add_nodes_from([0, 1, 2, 3, 4, 5, 6])
G.add_edges_from([
(0, 1),
(0, 2),
(0, 4),
(1, 3),
(2, 3),
(3, 4),
(3, 5),
(4, 6),
(5, 6),
])
nodePos = nx.circular_layout(G)
nx.draw(G, with_labels=True,pos=nodePos, font_color='white', font_weight='bold',
node_size=100,font_size=8)
plt.show()
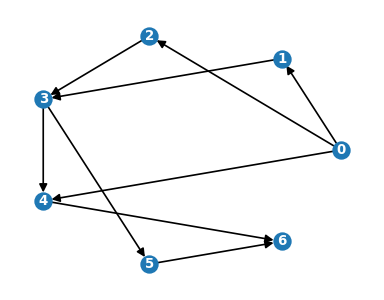
# przeszukiwanie w głąb
T = nx.depth_first_search.dfs_tree(G, 0)
nx.draw(G, with_labels=True,pos=nodePos,node_size=100,font_color='white',font_size=8)
nx.draw_networkx_edges(T, pos=nodePos,edge_color='r')
plt.show()
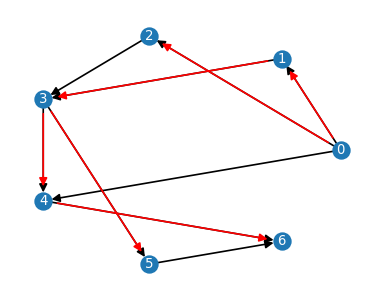
# przeszukiwanie wszerz
T = nx.breadth_first_search.bfs_tree(G, 0)
nx.draw(G, with_labels=True,pos=nodePos,node_size=100,font_color='white',font_size=8)
nx.draw_networkx_edges(T, pos=nodePos,edge_color='r')
plt.show()
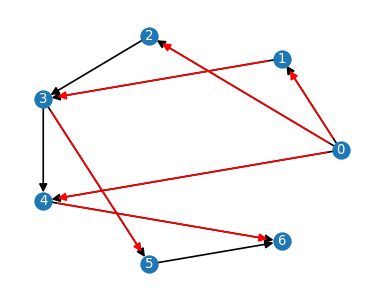
Możemy łatwo sprawdzić na powyższych rysunkach realizację alg. [5.2] i [5.3].
Kolejne algorytmy dotyczą grafów z wagami, rozdz. [5.8]. Tworzymy zatem przykładowy graf z wagami i znajdujemy najkrótszą ścieżkę między dwoma wierzchołkami:
G = nx.Graph()
G.add_nodes_from([1, 2, 3, 4, 5, 6])
G.add_weighted_edges_from([ # krawędzie z wagami
(1, 2, 7),
(2, 4, 15),
(4, 5, 6),
(5, 6, 9),
(6, 1, 14),
(1, 3, 9),
(2, 3, 10),
(3, 4, 11),
(3, 6, 2),
], weight='dist')
nodePos = nx.spring_layout(G)
label_weight=nx.get_edge_attributes(G,'dist')
nx.draw_networkx(G, pos=nodePos, with_labels=True,
node_size=100,font_color='white',font_size=8,font_weight='bold')
nx.draw_networkx_edge_labels(G, pos=nodePos, edge_labels=label_weight,font_size=8)
plt.axis("off")
plt.show()
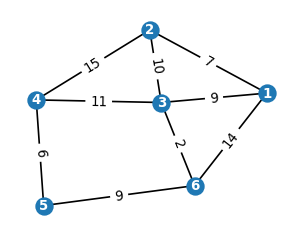
# najkrótsza ścieżka między wierzchołkami 1 i 5
P = nx.shortest_path(G, 1, 5, weight='dist')
print(P)
[1, 3, 6, 5]
# sumaryczna waga (długość) najkrótszej ścieżki
print(nx.shortest_path_length(G, 1, 5, weight='dist'))
20
# najkrótszą ścieżkę oznaczymy na czerwono
red_edges = list(zip(P,P[1:])) # zip stwarza odpowiednią krotkę z listy P
print(red_edges)
[(1, 3), (3, 6), (6, 5)]
sh=nx.Graph() # graf dla najkrótszej ścieżki
sh.add_nodes_from(P)
sh.add_edges_from(red_edges)
nx.draw_networkx(G, pos=nodePos, with_labels=True,
node_size=100,font_color='white',font_size=8,font_weight='bold')
nx.draw_networkx_edge_labels(G, pos=nodePos, edge_labels=label_weight,font_size=8)
nx.draw_networkx(sh, pos=nodePos,node_color='r',
node_size=100,font_color='white',font_size=8,font_weight='bold')
nx.draw_networkx_edges(sh, pos=nodePos, edge_color='r',width=3)
plt.axis("off")
plt.show()
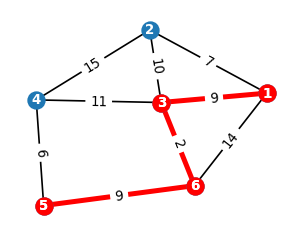
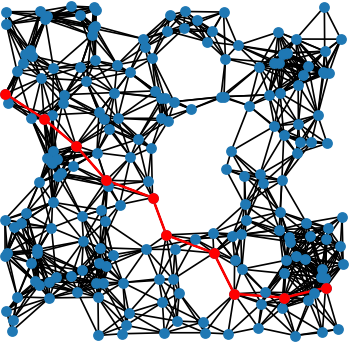
Grafy napotykane w „codziennym życiu” są na ogół bardzo duże (zob. wstęp rozdz. [5]). Poniżej przykład działania algorytmu znajdowania najkrótszej ścieżki dla dużego geometrycznego grafu losowego.
Geometryczny graf losowy
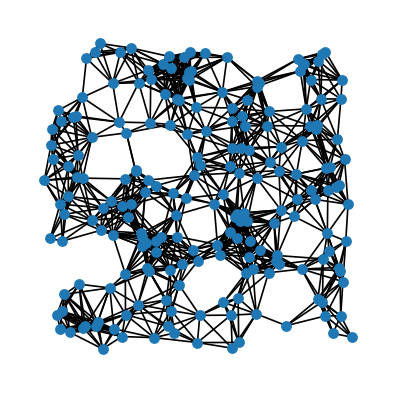
W konstrukcji geometrycznego grafu losowego umieszcza się jednorodnie losowo \(n\) wierzchołków w kwadracie \([0,1]\times[0,1]\). Dwa wierzchołki są łączone krawędzią, jeśli ich odległość jest mniejsza niż pewna zadana odległość \(d\).
# geometryczny graf losowy, n=200, d=0.15
G = nx.random_geometric_graph(200, 0.15)
pos = nx.get_node_attributes(G, 'pos')
plt.figure(figsize=(4,4))
nx.draw_networkx(G, pos=pos, with_labels=False,node_size=30)
plt.axis('off')
plt.show()
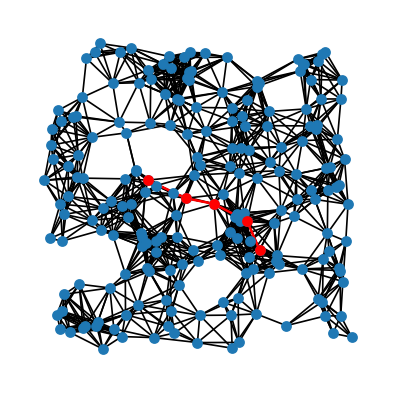
# najkrótsza ścieżka między wierzchołkami 1 i 50
P = nx.shortest_path(G, 10, 190)
red_edges = list(zip(P,P[1:]))
plt.figure(figsize=(4,4))
sh=nx.Graph()
sh.add_nodes_from(P)
sh.add_edges_from(red_edges)
nx.draw_networkx(G, pos=pos, with_labels=False,node_size=30)
nx.draw_networkx(sh, pos=pos,node_color='r',node_size=30,with_labels=False)
nx.draw_networkx_edges(sh, pos=pos, edge_color='r',width=1.5)
plt.axis('off')
plt.show()
ile_skl(G)
liczba składowych spójnych: 1
1
# drzewo spinające
T=wszerz(G)
plt.figure(figsize=(4,4))
#nx.draw_networkx(G, pos=pos, with_labels=False, node_size=30)
nx.draw_networkx(T, pos=pos, with_labels=False, node_size=30, edge_color='r')
plt.axis('off')
plt.show()

Średnica grafu
Średnica grafu to maksimum po wszystkich parach wierzchołków z ich najkrótszej odległości.
# średnica grafu (działa tylko dla grafu spójnego)
if ile_skl(G)==1:
print("średnica grafu:", nx.diameter(G))
liczba składowych spójnych: 1
średnica grafu: 11
Klika
Klika to podgraf pełny - każdy zna każdego!
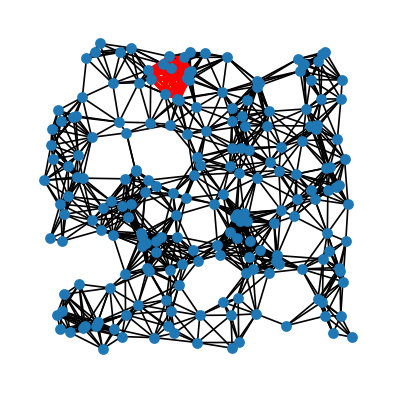
# największa klika
kli=list(nx.enumerate_all_cliques(G))[-1] # ostatni element listy klik
len(kli)
13
plt.figure(figsize=(4,4))
nx.draw_networkx(G, pos, with_labels=False, node_size=30)
nx.draw_networkx(G.subgraph(kli), pos, with_labels=False, node_size=8,
edge_color='r',width=1.5)
plt.axis("off")
plt.show()
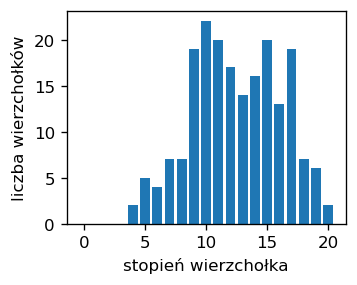
kG=nx.degree_histogram(G) # histogram stopni wierzchołków
plt.xlabel('stopień wierzchołka')
plt.ylabel('liczba wierzchołków')
plt.bar(range(len(kG)), kG)
plt.show()
Grafy z zewnętrznych danych¶
Częstokroć pragniemy zanalizowac dane z pomocą grafów. Dane są zebrane w plikach, więc pierwszym zadaniem jest wczytać i przekształcić je w odpowiedni format grafu. Poniżej przedstawiamy dwa popularne przykłady.
Sioux Falls¶
Ten przykład zaczerpniety jest ze strony https://github.com/bstabler/TransportationNetworks/tree/master/SiouxFalls i dotyczy analizy transportu w amerykańskim mieście Sioux Falls. Plik z danymi dot. położenia wierzchołków (skrzyżowań ulic) ma format
Node X Y ;
1 50000 510000 ;
2 320000 510000 ;
3 50000 440000 ;
4 130000 440000 ;
…. ,
gdzie \(X\) i \(Y\) są geograficznymi współrzędnymi. Wczytanie wierzchołków odbywa się nastepująco:
S=nx.Graph() # inicjalizacja grafu
f = open("SiouxFalls/SiouxFalls_node.tntp", "r")
line = f.readline() # opuść pierwszą linię
line = f.readline()
while len(line)-1: # jeśli linia nie jest pusta
line = line.strip(';') # usuń znak;
l = line.split() # utwórz z linii tablicę
node = int(l[0]) # nr wierzchołka
pos1 = float(l[1])/10000 # współrzędna x przeskalowana
pos2 = float(l[2])/10000 # współrzędna y przeskalowana
S.add_node(node, pos=(pos1,pos2)) # dodaj wierzchołek do grafu
line = f.readline() # przeczytaj nową linię
f.close()
print("liczba wierzchołków:", S.number_of_nodes())
liczba wierzchołków: 24
Format pliku z krawędziami ma postać
From To Volume Capacity Cost
1 2 4494.6576464564205 6.0008162373543197
1 3 8119.079948047809 4.0086907502079407
2 1 4519.079948047809 6.0008341229953821
2 6 5967.3363961713767 6.5735982553868011
… ,
gdzie pierwsze dwie kolumny podają wskaźniki wierzchołków, trzecia (Volume Capacity) to przepustowość komunikacyjna (w setkach samochodów na dobę) - tej wielkości nie używamy, a czwarta to koszt przejazdu.
f = open("SiouxFalls/SiouxFalls_flow.tntp", "r")
line = f.readline()
line = f.readline()
while len(line)-1:
l = line.split()
fromnode = int(l[0])
to = int(l[1])
volume = float(l[2])
cost = int(float(l[3]))
S.add_edge(fromnode, to, weight = cost) # dodaj krawędź do grafu, waga to koszt
line = f.readline()
f.close()
print("liczba krawędzi:", S.number_of_edges())
liczba krawędzi: 38
Mając zbudowany graf w oparciu o dane, możemy analizować go ptrzy pomocy posiadanych narzędzi, w szczególności możemy z pomocą wbudowanego algorytmu Dijkstry (zob. alg. [5.6]) znaleźć najkrótszą drogę między dwoma wybranymi wierzchołkami:
node_pos=nx.get_node_attributes(S,'pos') # położenia wierzchołków
arc_weight=nx.get_edge_attributes(S,'weight') # wagi krawędzi
sp = nx.dijkstra_path(S,source = 1, target = 19) # najkrótsza droga od 1 do 19
red_edges = list(zip(sp,sp[1:])) # lista czerwonych krawędzi
node_col = ['black' if not node in sp else 'red' for node in S.nodes()]
# czerwony kolor dla wierchołków na najkrótszej ścieżce, czarny poza
edge_col = ['black' if not edge in red_edges else 'red' for edge in S.edges()]
# czerwony kolor dla krawędzi na najkrótszej ścieżce, czarny poza
# rysunek, jak w uprzednich przypadkach
plt.figure(figsize=(3.5,5))
nx.draw_networkx(S, node_pos,node_color= node_col,
node_size=80,font_size=8,font_color="white",font_weight='bold')
nx.draw_networkx_edges(S, node_pos,edge_color= edge_col)
nx.draw_networkx_edge_labels(S, node_pos, edge_labels=arc_weight,font_size=8)
plt.axis('off')
plt.show()
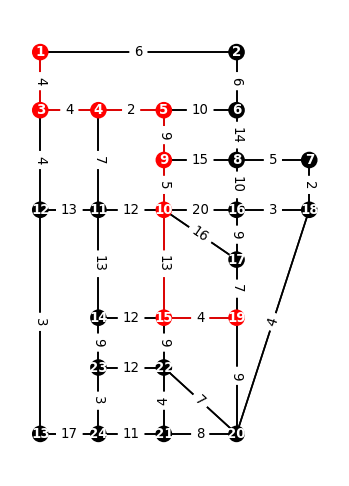
# najkrótsza ścieżka od 1 do 19
sp
[1, 3, 4, 5, 9, 10, 15, 19]
print("koszt całkowity wzdłóż optymalnej ścieżki:",
nx.dijkstra_path_length(S, 1, 19, 'weight'))
koszt całkowity wzdłóż optymalnej ścieżki: 41
Sieci społeczne¶
Drugi przykład pochodzi ze strony https://www.datacamp.com/community/tutorials/social-network-analysis-python i dotyczy sieci społecznej facebook. Wierzchołkami są osoby, które są połączone krawędzią jeśli są znajomymi. Plik z danymi ma bardzo prosty format, gdzie każda linia to para znajmych:
…
16 329
16 331
16 332
17 19
…
Osoba 16 zna osobe 329 itd. W tym przypadku możemy bardzo łatwo utworzyć graf poprzez instrukcję
G_fb=nx.read_edgelist("fb/facebook_combined.txt",
create_using = nx.Graph(), nodetype=int)
print(nx.info(G_fb)) # zwięzła informacja o grafie
Graph with 4039 nodes and 88234 edges
plt.figure(figsize=(5,5))
nx.draw_networkx(G_fb, with_labels=False,node_size=1,width=0.15)
plt.axis('off')
plt.show()
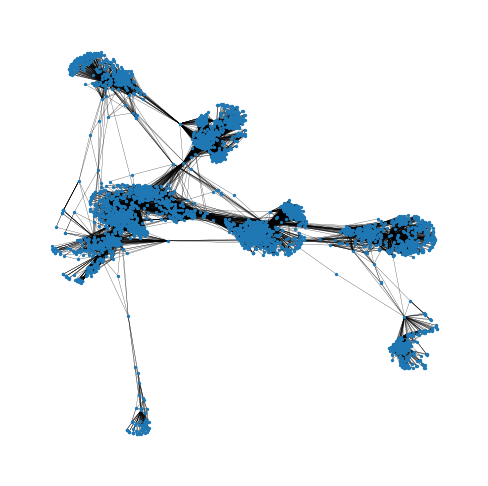
Zwróćmy uwagę na kilka wierzchołków o stosunkowo bardzo wysokim stopniu. W teorii sieci społecznych takie wierzchołki nazywamy „gwaizdowami” (stars).
Gh=nx.degree_histogram(G_fb)
plt.xlabel('stopień wierzchołka')
plt.ylabel('liczba wierzchołków')
plt.bar(range(len(Gh)), Gh,log=True, width=10)
plt.show()
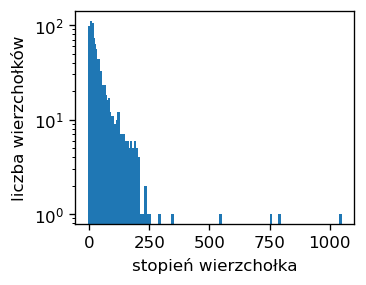
Kolorowanie grafów¶
Kolorowanie wierchołkowe grafów, opisane w rozdz. [5.12], uzyskujemy dzieki funcji equitable_color z biblioteki networkx:
G=nx.dodecahedral_graph() # przykładowy graf
kolo=nx.equitable_color(G, num_colors=4) # kolorowanie wierzchołków
kolo_list=list(kolo.values())
print(kolo)
print("")
print(kolo_list)
{0: 0, 1: 3, 2: 0, 3: 1, 4: 2, 5: 1, 6: 2, 7: 1, 8: 0, 9: 3, 10: 2, 11: 3, 12: 2, 13: 1, 14: 0, 15: 3, 16: 0, 17: 1, 18: 2, 19: 3}
[0, 3, 0, 1, 2, 1, 2, 1, 0, 3, 2, 3, 2, 1, 0, 3, 0, 1, 2, 3]
Wynikiem algorytmu jest słownik kolorów, numerowanych 0, 1, 2, …, który skonwertowaliśmy na listę. Wskaźnikom 0, 1, 2, … przydzielamy ulubione kolory:
colors=['red','blue','green','black','gray','brown','pink','yellow','orange','magenta']
Możemy teraz ładnie narysować pokolorowany graf:
cmap=[colors[kolo_list[i]] for i in range(len(kolo_list))]
nx.draw_circular(G, node_color = cmap, node_size=100,with_labels=True,
font_color='white', font_weight='bold',font_size=8)
plt.axis('equal') # zachowaj proporcje osi x i y
plt.axis('off')
plt.show()
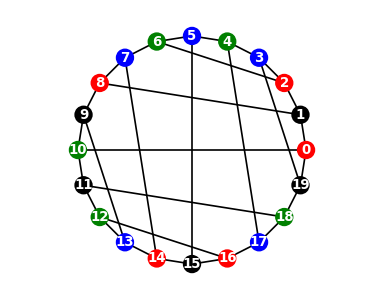
Przepływ w sieci¶
Do znajdowania maksymalnego przepływu w sieci o zadanych przepustowościach (zob. rozdz. [5.19]) służy funkcja maximum_flow z biblioteki networkx. Utwórzmy przykładową sieć:
G = nx.DiGraph()
G.add_edge('Z','a', capacity=3)
G.add_edge('Z','b', capacity=1)
G.add_edge('Z','d', capacity=1)
G.add_edge('a','c', capacity=3)
G.add_edge('b','c', capacity=5)
G.add_edge('b','d', capacity=4)
G.add_edge('d','e', capacity=2)
G.add_edge('c','U', capacity=2)
G.add_edge('e','U', capacity=3)
G.add_edge('e','b', capacity=1)
label_cap=nx.get_edge_attributes(G,'capacity') # etykieta krawędzi = przepustowość
nodePos = nx.spring_layout(G)
plt.figure(figsize=(3.5,3.5))
nx.draw_networkx(G, pos=nodePos, node_size=100, with_labels=True, font_color='white',
font_weight='bold',font_size=8)
nx.draw_networkx_edge_labels(G, pos=nodePos, edge_labels=label_cap,font_size=8);
plt.axis('off')
plt.show()

Znajdujemy teraz maksymalny przepływ między źródłem \(Z\) i ujściem \(U\):
flow_value, flow_dict = nx.maximum_flow(G, 'Z', 'U') # maksymalny przepływ
print("maksymalny przepływ:", flow_value)
print("")
print(flow_dict)
maksymalny przepływ: 4
{'Z': {'a': 2, 'b': 1, 'd': 1}, 'a': {'c': 2}, 'b': {'c': 0, 'd': 1}, 'd': {'e': 2}, 'c': {'U': 2}, 'e': {'U': 2, 'b': 0}, 'U': {}}
Należy teraz przekształcić powyższy słownik na graf, co czynimy w nastepujacy sposób:
tab=[]
F=nx.DiGraph()
for v in flow_dict:
for w in flow_dict.get(v):
tab.append((v,w,flow_dict.get(v).get(w)))
F.add_weighted_edges_from(tab)
Następnie rysujemy sieć z maksymalnym przepływem. Czarne etykiety oznaczają przepustowość krawedzi, a czerwone maksymalny przepływ.
label_fl=nx.get_edge_attributes(F,'weight') # etykiety maksymalnego przepływu
wid=[(1.5*i+0.4)/3 for i in list(nx.get_edge_attributes(F,'weight').values())]
# szerokość linii proporcjnalna do przepływu
# kolory dla wierzchołków
color_map = []
for node in G:
if node == 'Z' or node == 'U':
color_map.append('red')
else:
color_map.append('blue')
plt.figure(figsize=(3.5,3.5))
nx.draw_networkx(G, pos=nodePos, node_color = color_map, node_size=100,
with_labels=True, font_color='white', font_weight='bold',font_size=8, width=wid)
nx.draw_networkx_edge_labels(G, pos=nodePos, edge_labels=label_cap, label_pos=0.6,
font_size=8);
nx.draw_networkx_edge_labels(F, pos=nodePos, edge_labels=label_fl,label_pos=0.4,
font_color='red', font_weight='bold',font_size=8);
plt.title('Przepływ maksymalny',size=10)
plt.axis('off')
plt.show()
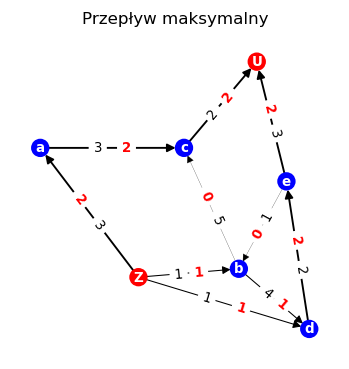
Znajdziemy teraz minimalny przekrój (por. tw. [5.31]):
mc=nx.minimum_cut(G, 'Z','U', capacity='capacity')
print(mc)
minp=mc[0]
(4, ({'c', 'a', 'b', 'd', 'Z'}, {'e', 'U'}))
color_map = [] # kolory dla wierzchołków
for node in G:
if node in mc[1][0]:
color_map.append('green')
else:
color_map.append('gray')
nx.draw_networkx(G, pos=nodePos, node_color = color_map, node_size=100, with_labels=True,
font_color='white', font_weight='bold', font_size=8, width=wid)
nx.draw_networkx_edge_labels(G, pos=nodePos, edge_labels=label_cap,
label_pos=0.6, font_size=8);
nx.draw_networkx_edge_labels(F, pos=nodePos, edge_labels=label_fl,
label_pos=0.4,font_color='red', font_size=8,font_weight='bold');
plt.title('Minimalny przekrój = '+str(mc[0]),size=10)
plt.axis('off')
plt.show()
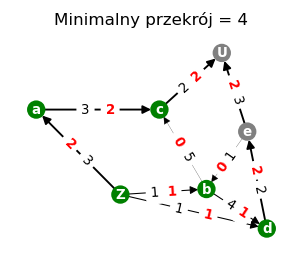
Wszystko się zgadza: maksymalny przepływ równa sie minimalnemu przekrojowi!
Drzewo Steinera¶
Uwaga!
Jest to inna koncepcja drzewa Steinera niż w książce. Nie szukamy tu położenia dodatkowych wierzchołków Steinera.
Problem drzewa Steinera
W spójnym grafie G z ustalonymi wagami szukamy minimalnego drzewa S zawierającego wszystkie zadane wierzchołki „terminalowe” T należące do G. ``
# przykładowy graf z wagami
G=nx.Graph()
G.add_weighted_edges_from([
(0, 1, 1),
(0, 2, 3),
(0, 3, 1),
(1, 2, 1),
(1, 3, 1),
(2, 3, 1),
(4, 2, 0.5),
(4, 1, 0.3),
(4, 0, 0.6)
])
# atrybuty
pos = nx.spring_layout(G)
weights = nx.get_edge_attributes(G,'weight')
labels = nx.get_node_attributes(G,'label')
T=[3,2,1] # wierzchołki "terminalowe" (drzewo S z definicji musi je zawierać)
# drzewo Steinera (uwaga: działa tylko dla grafów nieskierowanych)
S=nalg.steiner_tree(G, T ,weight='weight')
# kolory dla wierzchołków terminalowych
color_map = []
for node in G:
if node in T:
color_map.append('blue')
else:
color_map.append('gray')
nx.draw_networkx(G,pos,with_labels=True,node_size=100,font_color='white',
node_color = color_map,font_size=8)
nx.draw_networkx_edge_labels(G,pos,edge_labels=weights,font_size=8);
nx.draw_networkx_edges(S,pos,edge_color='r',width=2)
le=0
for e in S.edges:
le+=S.get_edge_data(*e)['weight'] # * zwraca tzw. "tuple form"
print("waga drzewa Steinera:", le)
plt.axis('off')
plt.show()
waga drzewa Steinera: 1.8

Widzimy, że drzewo Steinera S (czerwone krawędzie) zawiera wierzchołki terminalowe T (niebieskie) oraz dodatkowy wierzchołek 4. Jest to korzystne, bo droga z 1 do 2 jest krótsza prowadząc przez 4, gdzie 0.3+0.5=0.8, niż idąc bezpośrednio, gdzie długość wynosi 1.
Zadania¶
Narysuj średniej wielkości (ok. 10 wierzchołków i 20-30 krawędzi) graf spójny \(G\) na kartce papieru. Przydziel etykiety wierzchołkom i „wprowadź graf do komputera”. Narysuj graf.
Znajdź mininalne drzewo spinające grafu \(G\).
Przydziel wagi krawędziom grafu \(G\) i znajdź najkrótszą drogę między wybraną parą wierchołków.
Potraktuj wagi krawędzi \(G\) jako przepustowości sieci i znajdź maksymalny przepływ między dwoma wierzchołkami.
Zbadaj własności grafu nx.random_geometric_graph(200, d) w zależności od \(d \in (0,1)\), tj. spójność, liczbę krawędzi, rozmiar najwiekszej kliki.
Narysuj na kartce paperu sieć (na grafie skierowanym) o kilkunastu wierzchołkach, zadając przepustowości krawędzi. Zastosuj algorytm nx.maximum_flow do znalezienia maksymalnego przepływu.