Rekurencja¶
Standardowe biblioteki użyte w programie:
import numpy # numeryka
import math # funkcje matematyczne
import cmath # liczby zespolone
import random # liczby losowe
import time # pomiar czasu
import statistics as st # statystyka
import matplotlib.pyplot as plt # grafika
Wieże Hanoi ¶
Na początek klasyczny przykład algorytmu rekurencyjnego z rozdz. 1.1.
Etykiety krążków disc zdefiniowane są jako krotka („A”,”B”,”C”,”D”,…), gdzie potrzebujemy co najmniej tyle etykiet, ile wynosi używana później liczba krążków.
disc=("A","B","C","D","E") # użyjemy co najwyżej pięciu krążków
Poniższa funkcja realizuje algorytm rekurencyjny [1.1] (który tutaj wypisuje tylko kolejne instrukcje postępowania, tj. kroki algorytmu). Program han woła (dwakroć) sam siebie, zawsze z mniejszą o 1 liczbą krążków.
def han(n, init, fin, inter):
# n - liczba krążków
# init - pręt, na którym są początkowo krążki
# fin - pręt, na którym mają się na koniec znaleźć krążki
# inter - pręt pośredni
if n > 0: # wykonaj, jeśli są krążki
han(n-1, init, inter, fin) # przenieś n-1 krążków z init na inter
print("Przenieś krążek", disc[n-1], "z pręta", init, "na pręt", fin)
# przenieś krążek n z pręta init na fin (wypisz instrukcję)
han(n-1, inter, fin, init) # przenieś n-1 krążków z inter na fin
# wykonanie dla trzech krążków
han(3,"1","3","2")
Przenieś krążek A z pręta 1 na pręt 3
Przenieś krążek B z pręta 1 na pręt 2
Przenieś krążek A z pręta 3 na pręt 2
Przenieś krążek C z pręta 1 na pręt 3
Przenieś krążek A z pręta 2 na pręt 1
Przenieś krążek B z pręta 2 na pręt 3
Przenieś krążek A z pręta 1 na pręt 3
Powyżej możemy prześledzić dokładnie „historyjkę” z [Rys. 1.2].
# wykonanie dla czterech krążków
han(4,"1","2","3")
Przenieś krążek A z pręta 1 na pręt 3
Przenieś krążek B z pręta 1 na pręt 2
Przenieś krążek A z pręta 3 na pręt 2
Przenieś krążek C z pręta 1 na pręt 3
Przenieś krążek A z pręta 2 na pręt 1
Przenieś krążek B z pręta 2 na pręt 3
Przenieś krążek A z pręta 1 na pręt 3
Przenieś krążek D z pręta 1 na pręt 2
Przenieś krążek A z pręta 3 na pręt 2
Przenieś krążek B z pręta 3 na pręt 1
Przenieś krążek A z pręta 2 na pręt 1
Przenieś krążek C z pręta 3 na pręt 2
Przenieś krążek A z pręta 1 na pręt 3
Przenieś krążek B z pręta 1 na pręt 2
Przenieś krążek A z pręta 3 na pręt 2
Poniżej bardziej zaawansowana wersja, gdzie śledzimy kolejne stany (tj. ułożenia krążków) na prętach 1, 2, 3. Stany określone są jako łańcuchy znaków A, B, C, … etykietujących krążki, tak jak w rozdz. 1.1. Liczba kroków step określona jest jako global, ponieważ inicjalizujemy ją poza funkcją.
def han2(n, init, fin, inter):
# n - liczba krążków
# init - pręt, na którym są początkowo krążki
# fin - pręt, na którym mają się na koniec znaleźć krążki
# inter - pręt pośredni
global step # liczba kroków
if n > 0: # zrób, jeśli są krążki
han2(n-1, init, inter, fin) # przenieś n-1 krążków z init na inter
fin.append(init.pop())
step+=1 # licz kroki
print('krok',step,":")
print('1:',''.join(one))
print('2:',''.join(two))
print('3:',''.join(three))
han2(n-1, inter, fin, init) # przenieś n-1 krążków z inter na fin
# Stan początkowy: wszystkie trzy krążki na pręcie "1",
# od największego C do najmniejszego A
one = ['C', 'B', 'A']
two = []
three = []
step=0
print('krok', step, ":")
print('1:', ''.join(one))
print('2:', ''.join(two))
print('3:', ''.join(three))
han2(3, one, three, two)
krok 0 :
1: CBA
2:
3:
krok 1 :
1: CB
2:
3: A
krok 2 :
1: C
2: B
3: A
krok 3 :
1: C
2: BA
3:
krok 4 :
1:
2: BA
3: C
krok 5 :
1: A
2: B
3: C
krok 6 :
1: A
2:
3: CB
krok 7 :
1:
2:
3: CBA
Jeśli interesuje nas tylko liczba kroków algorytmu Hanoi, implementujemy rekurencję [1.1] w nastepujacy sposób:
# Ciąg Hanoi
def hanoi(n):
if n == 1:
return 1
else:
return 2*hanoi(n-1)+1
Możemy teraz sprawdzić równanie (1.2):
for n in range(1,10): print(n, hanoi(n), 2**n-1)
1 1 1
2 3 3
3 7 7
4 15 15
5 31 31
6 63 63
7 127 127
8 255 255
9 511 511
Pamiętacie mnichów buddyjskich? Przenoszą 64 złote krążki między diamentowymi prętami.
hanoi(64)
18446744073709551615
2**64-1
18446744073709551615
# zakładamy, że jeden ruch trwa 5 sekund i przeliczamy czas na lata
x = (2**64-1)*5/60/60/24/365
# format liczby z wykładnikiem
y = '%.1E' % x
print("czas pracy mnichów:",y,"lat")
w=13.7*10**9 # wiek Wszechświata
print(round(x/w),"razy dłużej od wieku Wszechświata")
czas pracy mnichów: 2.9E+12 lat
213 razy dłużej od wieku Wszechświata
Rekurencja z zadania [1.10] posiada \(n^2\) w miejsce \(1\), co prowadzi do oczywistej modyfikacji:
# ciąg Hanoi, gdzie liczymy przeniesioną masę krążków
# krążek n ma masę n**2
def hanoi_m(n):
if n == 1:
return 1
else:
return 2*hanoi_m(n-1)+n**2 # tutaj modyfikacja
[hanoi_m(n) for n in range(1,11)] # tablica 10 pierwszych wyrazów
[1, 6, 21, 58, 141, 318, 685, 1434, 2949, 5998]
Ciąg Fibonacciego¶
Ciąg Fibonacciego [1.8] programujemy analogicznie do powyższych przykładów:
def fib(n):
if n == 1:
return 1
elif n==2:
return 1
else:
return fib(n-1)+fib(n-2) # suma dwóch poprzednich wyrazów
fib(9)
34
[fib(i) for i in range(1, 11)]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
Kolejne ilorazy \(F_{i+1}/F_i\), zaokrąglone do 6 cyfr znaczących:
[round(fib(i+1)/fib(i),6) for i in range(1,16)]
[1.0,
2.0,
1.5,
1.666667,
1.6,
1.625,
1.615385,
1.619048,
1.617647,
1.618182,
1.617978,
1.618056,
1.618026,
1.618037,
1.618033]
Jak wiemy z równ. [1.26], powyższe ilorazy dążą do Złotego Podziału \(\phi\) [1.27]:
phi=(1+math.sqrt(5))/2.
print(phi)
1.618033988749895
Jeśli chcemy utworzyć tablicę kolejnych wyrazów ciągu Fibonacciego, postępujemy następująco:
fi=[] # pusta tablica
fi.append(1) # pierwszy wyraz
fi.append(1) # drugi wyraz
for i in range(2,20):
fi.append(fi[i-2]+fi[i-1]) # kolejne wyrazy
print(fi)
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765]
Metoda równana charakterystycznego¶
(dla rekurencji liniowej rzędu 2, rozdz. 1.5)
Zakładamy, że rekurencja dla ciągu \(f_n\) ma postać
\(a f_n + b f_{n-1} + c f_{n-2} = 0\) (przy czym stała a jest różna od 0),
np. dla ciagu Fibonacciego \(a=1, b=-1, c=-1\). Rekurencja rzędu 2 wymaga dwóch warunków „początkowych”, znamy zatem dwa różne wyrazy ciagu, \(n\) i \(m\). Słowo „początkowych” ujęte jest w cudzysłów, bowiem niekoniecznie \(n=1\), \(m=2\), jak w przypadku ciągu Fibonacciego. Wskaźniki \(n\) i \(m \neq n\) mogą być dowolne i wynikają z natury konkretnego problemu.
Poniższe pomocnicze funkcje obliczają wyróżnik równania kwadratowego \(\Delta\) oraz jego pierwiastki:
# delta dla równania kwadratowego
def de(a, b, c):
return b*b-4*a*c
# pierwiastki równania kwadratowego
def x1x2(a, b, c):
d=de(a,b,c) # wyróżnik
if d>0: # dla d>0 pierwiastki są rzeczywiste
return [(-b+math.sqrt(d))/(2*a),(-b-math.sqrt(d))/(2*a)]
if d<0: # dla d<0 pierwiastki są zespolone
return [(-b+cmath.sqrt(d))/(2*a),(-b-cmath.sqrt(d))/(2*a)] # biblioteka cmath
if d==0: # dla d=0 jest jeden podwójny pierwiastek rzeczywisty
return -b/(2*a)
Oto poszczególne przypadki (symbol j oznacza w bibiotece cmath jednostkę urojoną):
print(de(1,3,1), x1x2(1,3,1))
print(de(1,2,2), x1x2(1,2,2))
print(de(1,2,1), x1x2(1,2,1))
5 [-0.3819660112501051, -2.618033988749895]
-4 [(-1+1j), (-1-1j)]
0 -1.0
Liczby zespolone wprowadzamy używając symbolu j, np. w następujący sposób:
1j**2
(-1+0j)
Algorytm [1.2] programujemy w nastepujący sposób:
def sol_rec(a,b,c,n,an,m,am,i):
"""
Rozwiąż rekurencję liniową rzędu 2
input:
a, b, c - parametry (a różne od 0)
n - wskaźnik jednego znanego wyrazu
an - jego wartość
m - wskaźnik drugiego znanego wyrazu (n różne od m)
am - jego wartość
i - wskaźnik szukanego wyrazu
output:
wartość wyrazu i
"""
if de(a,b,c) != 0: # dwa różne pierwiastki (delta różna od 0)
[x1, x2]=x1x2(a, b, c)
# ogólne rozwiązanie na stałe c1 i c2
c1=(an*x2**m - am*x2**n)/(x1**n*x2**m - x1**m*x2**n)
c2=(-an*x1**m + am*x1**n)/(x1**n*x2**m - x1**m*x2**n)
return c1*x1**i+c2*x2**i # ogólna postać wyrazu i
else: # jeden pierwiastek (delta=0)
x=x1x2(a, b, c)
# ogólne rozwiązanie na stałe c1 i c2
c1=((am*n)/x**m - (an*m)/x**n)/(n - m)
c2=(am/x**m - an/x**n)/(m - n)
return (c1+c2*i)*x**i # ogólna postać wyrazu i
Poniżej sprawdzenie dla ciągu Fibonacciego. Ponieważ wiemy, że wyrazy ciągu są liczbami całkowitymi, w celu uzyskania czytelniejszego wydruku stosujemy funkcje real oraz int.
[int(sol_rec(1,-1,-1,1,1,2,1,i)).real for i in range(1,11)]
[0, 0, 1, 2, 4, 8, 13, 21, 34, 55]
Inne przykłady:
def round_complex(x): # zaokrąglanie liczb zespolonych
return complex(round(x.real),round(x.imag))
[int(round_complex(sol_rec(1,-1,1,1,1,2,1,i)).real) for i in range(1,11)]
[1, 1, 0, -1, -1, 0, 1, 1, 0, -1]
[round(sol_rec(1,2,1,1,1,2,1,i)) for i in range(1,11)]
[1, 1, -3, 5, -7, 9, -11, 13, -15, 17]
[int(round_complex(sol_rec(1,-3,3,1,1,2,1,i)).real) for i in range(1,17)]
[1, 1, 0, -3, -9, -18, -27, -27, 0, 81, 243, 486, 729, 729, 0, -2187]
Błądzenia przypadkowe¶
Liczby pseudolosowe¶
Symulowanie procesów stochastycznych wymaga zastosowania liczb pseudolosowych, wbudowanych we wszystkie zaawansowane języki programowania. Zaczynamy od przykładu kostki do gry (3.1), używając biblioteki random.
# kostka do gry: losowa liczba naturalna w zakresie od 1 do 6
random.randint(1,6)
6
Rzucamy 600000 razy i tworzymy histogram (por. rys. 3.1):
# zbieramy wyniki kolejnych rzutów w tablicy
t=[random.randint(1,6) for i in range(600000)]
plt.figure(figsize=(3,2),dpi=120) # rozmiar grafiki
plt.tick_params(axis='both', which='major', labelsize=7) # rozmiar znaczników osi
plt.hist(t, bins=50, facecolor='green')
plt.show()
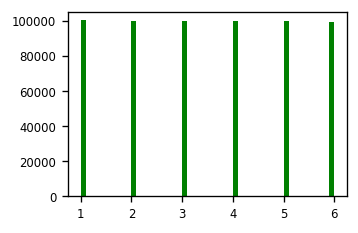
Widzimy, że każde oczko wypada po około 100000, czyli kostka jest dobra (niesfałszowana!).
Ruina gracza¶
W problemie ruiny gracza (rozdz. 1.7) losowanie odbywa się „sfałszowaną” monetą, gdzie prawdopodobieństwo uzyskania orła wynosi \(p\), a reszki \(q=1-p\). Poniżej tworzymy generator liczb losowych, który zwraca 1 z prawdopodobieństwem \(p\) oraz -1 z prawdopodobieństwem \(q\). Uzyskanie 1 oznacza przejście do stanu posiadania większego o 1, a -1 do stanu posiadania mniejszego o 1 (zob. rys. 1.8).
def coin(p):
# zwróć 1 z prawdopodobieństwem p lub -1 z prawdopodobieństwem q=1-p
if random.uniform(0,1)<p: # gdy liczba losowa rozłożona jednorodnie
# w przedziale (0,1) jest mniejsza od p
# (tj. prawdopodobientwo tegoż wynosi p)
return 1 # zwróć 1
else: # w przeciwnym razie
return -1 # zwróć -1
Sprawdzamy teraz działanie funkcji coin (analogicznie jak dla kostki do gry powyżej). Parametr weights zmienia wysokość słupków tak, aby odpowiadała ona względnej częstości uzyskania 1 lub -1.
p=0.4 # prawdopodobieństwo orła
nu=100000 # liczba rzutów
t=[coin(p) for k in range(1,nu)]
plt.figure(figsize=(3,2),dpi=120) # rozmiar grafiki
plt.tick_params(axis='both', which='major', labelsize=7) # rozmiar znaczników osi
plt.hist(t, bins=30, facecolor='green',weights=1/nu*numpy.ones_like(t))
plt.show()
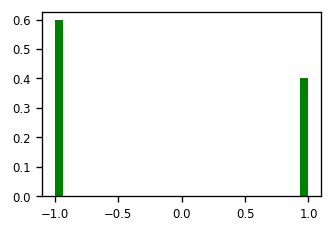
Pełna symulacja ruiny gracza jest nastepująca:
time0 = time.time() # czas startu do pomiaru czasu wykonania programu
n = 40000 # maksymalna liczba kroków (tj. pojedynczych gier dla jednego gracza)
p = 0.495 # prawdopodobieństwo wygrania w pojedynczej grze (uzyskania orła)
q = 1-p # prawdopodobieństwo przegrania w pojedynczej grze
players = 200 # całkowita liczba graczy
players_b = 0 # aktualna liczba graczy, którzy rozbili bank
start = 100 # początkowa liczba monet u każdego z graczy
fin = 200 # liczba monet u gracza, przy której następuje rozbicie banku
x = list(range(n)) # współrzędne x (nr kroku, tj. kolejnej pojedynczej gry)
# ustawienia rysunku
plt.figure(figsize=(20,3)) # rozmiar
plt.title("Ruina gracza, p=" + str(p),fontsize=24) # tytuł
plt.xlim(0,n-1) # zakresy osi
plt.ylim(0,fin)
plt.xlabel('krok',fontsize=24) # etykiety osi
plt.ylabel('stan posiadania',fontsize=24)
plt.tick_params(axis='both', which='major', labelsize=16) # rozmiar znaczników osi
# losowe kolory RGB dla poszczególnych graczy
col = [(random.uniform(0,1),random.uniform(0,1),random.uniform(0,1))
for _ in range(players)]
# czasy gry dla wszystkich, tych co rozbili bank i tych, co się spłukali
ti=[]
ti_b=[]
ti_0=[]
for k in range(players): # pętla po graczach
y = numpy.zeros(n) # inicjalizacja macierze
i=0 # początek gry, krok 0
y[0]=start # stan posiadania w kroku 0
while i < n-1:
i+=1 # kolejny krok
y[i]=y[i-1] + coin(p) # posiadanie losowo zwieksza się lub zmniejsza o 1
if y[i]==0: # jeśli spłukany po i grach
ti_0.append(i) # zapisz liczbę kroków (czas gry)
break # wyjdź
if y[i]==fin: # jeśli rozbił bank po i grach
players_b+=1 # zwiększ o 1 liczbę graczy, którzy rozbili bank
ti_b.append(i) # zapisz liczbę kroków (czas gry)
break # wyjdź
plt.scatter(x, y, s=0.01, label=str(k+1)) # zrób wykres dla gracza k
ti.append(i) # zapisz czas gry
lw= max(ti) # najdłuższy czas gry
plt.xlim(0,1.1*lw) # zakres osi x o 10% dłuzszy od najdłuższego czsu gry
# wstawka tekstowa do rysunku
plt.text(x=0.85*lw, y=80, s="spłukanych "+str(len(ti_0)),fontsize=24, color='red')
plt.text(x=0.85*lw, y=120, s="rozbiło bank "+str(len(ti_b)),fontsize=24, color='blue')
# pomiar czasu umożliwia oszacowanie jak długo potrwają obliczenia przy wydłużeniu danych
# w naszym przypadku rośnie on liniowo z liczbą graczy
time1 = time.time()
print("czas wykonania symulacji:", round(time1 - time0, 1),"s")
plt.show()
czas wykonania symulacji: 25.3 s
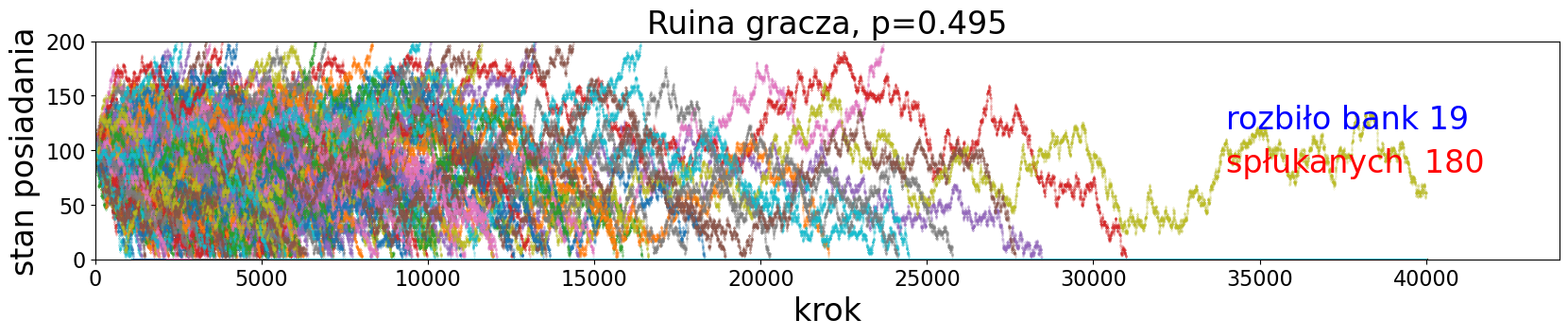
Możemy porównać oszacowane z powyższej symulacji prawdopodobienstwo rozbicia banku (równe stosunkowi liczby graczy, którzy rozbili bank, do wszystkich graczy), z dokładnym wzorem na prawdopodobieństwo [1.45]:
print("oszacowane z symulacji prawd. rozbicia banku =",round(players_b/players,2),
"\npowinno być (dla b. dużej liczby graczy)",round((1-(q/p)**start)/(1-(q/p)**fin),2))
oszacowane z symulacji prawd. rozbicia banku = 0.1
powinno być (dla b. dużej liczby graczy) 0.12
Podobnie, oszacowany średni czas gry porównyjemy do wzoru (1.48):
print("średni czas gry:",round(st.mean(ti),1),", powinno być (dla b. dużej liczby graczy) ",
round((-fin*(q/p)**start+start*(q/p)**fin)/(1-(q/p)**fin)/(p-q),1))
print("średni czas gry dla tych, co rozbili bank:",round(st.mean(ti_b),1))
print("średni czas gry dla tych, co się spłukali:",round(st.mean(ti_0),1))
średni czas gry: 7524.3 , powinno być (dla b. dużej liczby graczy) 7429.5
średni czas gry dla tych, co rozbili bank: 8864.4
średni czas gry dla tych, co się spłukali: 7202.4
Widzimy, że średni czas gry dla graczy, którzy rozbili bank, jest dłuższy niż dla tych, co się spłukali (co jest intuicyjne dla \(p<0.5\)).
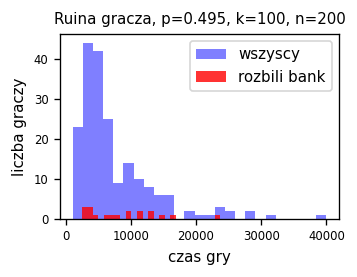
Ciekawe jest popatrzyć na rozkład czasów gry dla poszczególnych graczy (por. **rys. [1.11]):
plt.figure(figsize=(3,2),dpi=120) # rozmiar grafiki
num_bins = 25 # liczba przedziałów histogramu
plt.hist(ti, num_bins, facecolor='blue', alpha=0.5,label="wszyscy")
plt.hist(ti_b, num_bins, facecolor='red', alpha=0.8,label="rozbili bank")
plt.title("Ruina gracza, p="+str(p)+", k="+str(start)+", n="+str(fin),fontsize=9)
plt.xlabel('czas gry',fontsize=9)
plt.ylabel('liczba graczy',fontsize=9)
plt.tick_params(axis='both', which='major', labelsize=7) # rozmiar znaczników osi
plt.legend(prop={'size':9}) # legenda
plt.show()
Silnia jako rekurencja¶
Obliczamy rekurencyjnie silnię:
def fact(n):
if n == 0:
return 1
else:
return n*fact(n-1)
fact(7)
5040
# biblioteki matematyczne Pythona mają wbudowaną silnię, np.
math.factorial(7)
5040
Sprawdzimy teraz, jak działa wzór Stirlinga z poprawką [2.9] (bierzemy tylko jeden człon poprawki \(1/12n\)):
def stirling(n):
return math.sqrt(2*math.pi*n)*(n/math.e)**n*(1+1/(12*n))
for n in range(1,20):
print(n,math.factorial(n),
round((stirling(n)-math.factorial(n))/math.factorial(n)*100,3),"%")
1 1 -0.102 %
2 2 -0.052 %
3 6 -0.028 %
4 24 -0.017 %
5 120 -0.012 %
6 720 -0.008 %
7 5040 -0.006 %
8 40320 -0.005 %
9 362880 -0.004 %
10 3628800 -0.003 %
11 39916800 -0.003 %
12 479001600 -0.002 %
13 6227020800 -0.002 %
14 87178291200 -0.002 %
15 1307674368000 -0.001 %
16 20922789888000 -0.001 %
17 355687428096000 -0.001 %
18 6402373705728000 -0.001 %
19 121645100408832000 -0.001 %
Widzimy, że przybliżenie działa bardzo dokładnie, do ułamka procenta, nawet dla małych \(n\). Uwzględnienie kolejnych członów we wzorze [2.9] jeszcze bardziej ulepsza wynik.
Rekurencja w dwóch wymiarach ¶
Symbol Newtona¶
Skonstruujemy trójkąt Pascala, rys. 2.7 (pamietamy, że „+” łączy listy):
newton=[] # inicjalizacja pustej tablicy
# dodanie [1] jako elementu 0 tablicy
newton.append([1])
# zrobimy 12 wierszy
for n in range(1,12):
# wiemy, że po bokach są jedynki, stąd [1]+ i +[1]
# w środku pętla po k daje (n-1) elementów
# każdy jest sumą elemntów z wiersza wyżej w pozycji k-1 oraz k
newton.append([1]+[newton[n-1][k-1]+newton[n-1][k] for k in range(1,n)]+[1])
Tablica newton jest dwuwymiarowa:
newton
[[1],
[1, 1],
[1, 2, 1],
[1, 3, 3, 1],
[1, 4, 6, 4, 1],
[1, 5, 10, 10, 5, 1],
[1, 6, 15, 20, 15, 6, 1],
[1, 7, 21, 35, 35, 21, 7, 1],
[1, 8, 28, 56, 70, 56, 28, 8, 1],
[1, 9, 36, 84, 126, 126, 84, 36, 9, 1],
[1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1],
[1, 11, 55, 165, 330, 462, 462, 330, 165, 55, 11, 1]]
Ładniejszy wydruk uzyskujemy poprzez sformatowane wypisywanie:
for n in range(12):
row_format ="{:>4}" * (n+1)
print((12-n)*" ",row_format.format(*newton[n]))
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
Sprawdzamy, że suma elementów w wierszu trójkąta Pascala daje \(2^n\), zgodnie ze wzorem [2.14]:
for n in range(12):
print(sum(newton[n]),2**n)
1 1
2 2
4 4
8 8
16 16
32 32
64 64
128 128
256 256
512 512
1024 1024
2048 2048
Podobnie, suma elementów w wierszu trójkąta Pascala mnożonych naprzemiennie przez \(-1\) daje 0, zgodnie ze wzorem [2.15]:
for n in range(12):
s=0
for k in range(n+1):
s=s+newton[n][k]*(-1)**k
print(s)
1
0
0
0
0
0
0
0
0
0
0
0
A teraz liczby Fibonacciego, ukryte w trójkacie Pascala wg rys. [2.12]:
for n in range(12):
s=0
for k in range(n//2+1):
s=s+newton[n-k][k]
print(s)
1
1
2
3
5
8
13
21
34
55
89
144
Liczby Stirlinga I rodzaju (cyklowe)¶
Wzory wzięte są z tw. 4.1. Procedura jest programistycznie analogiczna do trójkąta Pascala, jedynie po lewej stronie mamy [0] i rekurencja ma inną postać:
stir_c=[]
stir_c.append([1])
for n in range(1,12):
stir_c.append([0]+[stir_c[n-1][k-1]+(n-1)*stir_c[n-1][k] for k in range(1,n)]+[1])
for n in range(9):
row_format ="{:>6}" * (n+1)
print(row_format.format(*stir_c[n]))
1
0 1
0 1 1
0 2 3 1
0 6 11 6 1
0 24 50 35 10 1
0 120 274 225 85 15 1
0 720 1764 1624 735 175 21 1
0 5040 13068 13132 6769 1960 322 28 1
Suma elementów w wierszu daje n! - liczbę wszystkich permutacji:
for n in range(0,12):
print(sum(stir_c[n]),math.factorial(n))
1 1
1 1
2 2
6 6
24 24
120 120
720 720
5040 5040
40320 40320
362880 362880
3628800 3628800
39916800 39916800
Suma elementów w wierszu mnożonych naprzemiennie przez \(-1\) daje 0, począwszy od \(n=2\)
for n in range(12):
s=0
for k in range(n+1):
s=s+stir_c[n][k]*(-1)**k
print(s)
1
-1
0
0
0
0
0
0
0
0
0
0
Liczby Stirlinga II rodzaju (podziałowe)¶
Teraz bierzemy wzory z tw. 4.2:
stir_p=[]
stir_p.append([1])
for n in range(1,12):
stir_p.append([0]+[stir_p[n-1][k-1]+k*stir_p[n-1][k] for k in range(1,n)]+[1])
for n in range(10):
row_format ="{:>5}" * (n+1)
print(row_format.format(*stir_p[n]))
1
0 1
0 1 1
0 1 3 1
0 1 7 6 1
0 1 15 25 10 1
0 1 31 90 65 15 1
0 1 63 301 350 140 21 1
0 1 127 966 1701 1050 266 28 1
0 1 255 3025 7770 6951 2646 462 36 1
Sumy w poszczególnych wierszach tworzą liczby Bella, zgodnie ze wzorem [4.6]:
for n in range(12):
print(n,sum(stir_p[n]))
0 1
1 1
2 2
3 5
4 15
5 52
6 203
7 877
8 4140
9 21147
10 115975
11 678570
Zadania¶
Wszystkie zadania dotyczą programowania w Pythonie. Zadania „teoretyczne” znajduja się w podstawowej części książki.
Rozwiaż zad. [1.1] z pomocą funkcji sol_rec.
Utwórz funkcję realizującą rekurencję pierwszego rzędu z członem niejednorodnym postaci \(a+b n\) i rozwiąż numerycznie problem dzielenia pizzy z zad. [1.2]).
Wygeneruj liczby Fibonacciego i sprawdź numerycznie wszystkie przypadki z zad. [1.5] oraz [1.6].
Utwórz funkcję realizującą rekurencję z zad. [1.12].
Zmodyfikuj kod dla Ruiny gracza z wykładu, aby rozwiązać zad. [1.21], [1.22] i [1.23].
Oblicz i narysuj trójkąt liczb Bella z rys. [4.5].
Oblicz i narysuj trójkąt partycji \(p(n,k)\) ze wzoru [4.20], rys. [4.11].
Oblicz i narysuj trójkąt partycji \(q(n,k)\) ze wzoru [4.24], rys. [4.13].
Uruchom program ilustrujący algorytm Kratsuby-Ofmana (rozdz. [1.8]) ze strony www.codeandgadgets.com/karatsuba-multiplication-python/ i przedyskutuj wyniki.