Interpolacja¶

Symulowane dane¶

Do tej pory zajmowaliśmy się klasyfikacją, czyli rozpoznawaniem przez sieci, czy dany obiekt (w naszym przykładzie punkt na płaszczyźnie) ma określone cechy. Teraz przechodzimy do innego praktycznego zastosowania, a mianowicie do interpolacji funkcji. To zastosowanie ANN stało się bardzo popularne w analizie danych naukowych. Zilustrujemy tę metodę na prostym przykładzie, który wyjaśni podstawową ideę i pokaże, jak ona działa.

Wyobraźmy sobie, że dysponujemy pewnymi danymi eksperymentalnymi. W tym przypadku symulujemy je w sztuczny sposób, np.

def fi(x):
    return 0.2+0.8*np.sin(x)+0.5*x-3 # a function

def data(): 
    x = 7.*np.random.rand() # random x coordinate
    y = fi(x)+0.4*func.rn() # y coordinate = the function value + noise from [-0.2,0.2]
    return [x,y]

Powinniśmy teraz myśleć w kategoriach uczenia nadzorowanego: \(x\) to „cecha”, a \(y\) to „etykieta”.

Tablicujemy nasze zaszumione punkty danych i wykreślamy je wraz z funkcją fi(x), wokół której się wahają. Jest to imitacja pomiaru eksperymentalnego, który zawsze obarczony jest pewnym błędem, tutaj naśladowanym przez losowy szum.

tab=np.array([data() for i in range(200)])    # data sample
features=np.delete(tab,1,1)                   # x coordinate
labels=np.delete(tab,0,1)                     # y coordinate

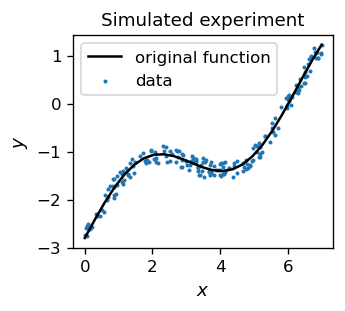
W języku ANN mamy zatem próbkę treningową składającą się z punktów o danych wejściowych (cechach) \(x\) i „prawdziwych” danych wyjściowych (etykietach) \(y\). Tak jak poprzednio, minimalizujemy funkcję błędu odpowiedniej sieci neuronowej,

\[E(\{w \}) = \sum_p (y_o^{(p)} - y^{(p)})^2. \]

Ponieważ generowane \(y_o\) jest pewną (zależną od wag) funkcją \(x\), metoda ta jest odmianą dopasowania najmniejszych kwadratów, powszechnie stosowaną w analizie danych. Różnica polega na tym, że w standardowej metodzie najmniejszych kwadratów funkcja modelu, którą dopasowujemy do danych, ma pewną prostą postać analityczną (np. \( f(x) = A + B x\)), podczas gdy teraz jest to pewna „zakamuflowana” funkcja zależna od wag, dostarczona przez sieć neuronową.

Interpolacja z pomocą ANN¶

Aby zrozumieć podstawową ideę, rozważmy sieć z tylko dwoma neuronami w warstwie pośredniej, z sigmoidalną funkcją aktywacji:

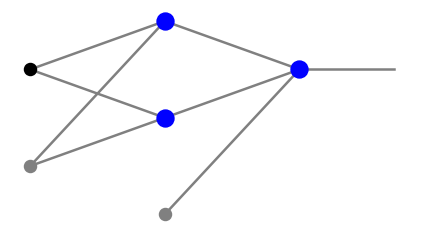
Sygnały docierające do dwóch neuronów w warstwie środkowej to, w notacji z rozdz. Więcej warstw,

\[ s_1^{1}=w_{01}^{1}+w_{11}^{1} x, \]

\[ s_2^{1}=w_{02}^{1}+w_{12}^{1} x, \]

a sygnały wychodzące to odpowiednio,

\[ \sigma \left( w_{01}^{1}+w_{11}^{1} x \right), \]

\[ \sigma \left( w_{02}^{1}+w_{12}^{1} x \right). \]

Zatem połączony sygnał wchodzący do neuronu wyjściowego ma postać

\[ s_1^{2}=w_{01}^{2}+ w_{11}^{2}\sigma \left( w_{01}^{1}+w_{11}^{1} x \right) + w_{21}^{2}\sigma \left( w_{02}^{1}+w_{12}^{1} x \right). \]

Przyjmując, dla ilustracji, przykładowe wartości wag

\[ w_{01}^{2}=0, w_{11}^{2}=1, w_{21}^{2}=-1, w_{21}^{2}, w_{11}^{1}=w_{12}^{1}=1, \, w_{01}^{1}=-x_1, \, w_{02}^{1}=-x_2, \]

gdzie \(x_1\) i \(x_2\) to notacja skrótowa, otrzymujemy

\[ s_1^{2}=\sigma(x-x_1)-\sigma(x-x_2). \]

Funkcja ta jest przedstawiona na poniższym wykresie, gdzie \(x_1=-1\) i \(x_2=4\). Dąży ona do 0 w \(-\infty\), potem rośnie wraz z \(x\), osiągając maksimum w punkcie \((x_1+x_2)/2\), a następnie maleje, dążąc do 0 przy \(+\infty\). W punktach \(x=x_1\) i \(x=x_2\) jej wartości wynoszą około 0.5, można więc powiedzieć, że przedział znaczących wartości funkcji zawiera się między \(x_1\) i \(x_2\).

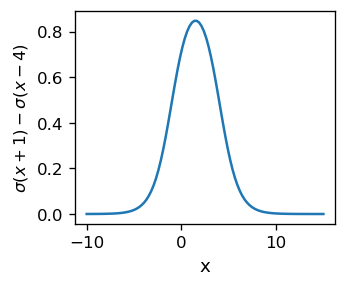
Jest to prosty, ale ważny wniosek: Jesteśmy w stanie utworzyć, za pomocą pary neuronów z sigmoidami, sygnał „garbowy”, zlokalizowany wokół danej wartości, tutaj \( (x_1 + x_2) / 2 = 2\), i o danym rozrzucie rzędu \(|x_2-x_1|\). Zmieniając wagi, możemy modyfikować jej kształt, szerokość i wysokość.

Można teraz pomyśleć w następujący sposób: Wyobraźmy sobie, że mamy do dyspozycji wiele neuronów w warstwie pośredniej. Możemy je łączyć w pary, tworząc garby „specjalizujące się” w określonych regionach współrzędnych. Następnie, dostosowując wysokości garbów, możemy łatwo aproksymować daną funkcję.

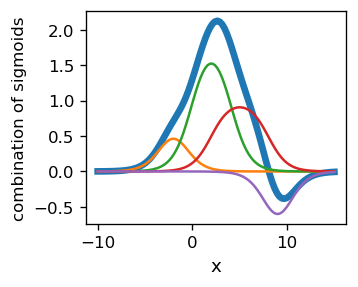
W rzeczywistej procedurze dopasowania nie musimy „łączyć neuronów w pary”, lecz dokonać łącznego dopasowania wszystkich parametrów jednocześnie, tak jak to miało miejsce w przypadku klasyfikatorów. Poniższy przykład przedstawia kompozycję 8 sigmoidów,

\[ f = \sigma(z+3)-\sigma(z+1)+2 \sigma(z)-2\sigma(z-4)+ \sigma(z-2)-\sigma(z-8)-1.3 \sigma(z-8)-1.3\sigma(z-10). \]

Na rysunku funkcje składowe (cienkie linie oznaczające pojedyncze garby) sumują się do funkcji o dość skomplikowanym kształcie, oznaczonej grubą linią.

Informacja

Jeśli dopasowana funkcja jest regularna, można ją aproksymować za pomocą kombinacji liniowej sigmoidów. W przypadku większej liczby sigmoidów można uzyskać lepszą dokładność.

Istnieje istotna różnica między ANN używanymi do aproksymacji funkcji w porównaniu z omawianymi wcześniej klasyfikatorami binarnymi. Tam odpowiedzi były równe 0 lub 1, więc w warstwie wyjściowej stosowaliśmy skokową funkcję aktywacji, a raczej jej gładką odmianę sigmoidalną. W przypadku aproksymacji funkcji odpowiedzi stanowią zazwyczaj kontinuum w zakresie wartości funkcji. Z tego powodu w warstwie wyjściowej używamy po prostu funkcji identycznościowej, czyli przepuszczamy przez nią bez zmian przychodzący sygnał. Oczywiście sigmoidy pozostają w warstwach pośrednich. Wówczas wzory używane do algorytmu backprop z sekcji Algorytm propagacji wstecznej (backprop) mają w warstwie wyjściowej \(f_l(s)=s\).

Warstwa wyjściowa dla aproksymacji funkcji

W sieciach ANN używanych do aproksymacji funkcji, funkcja aktywacji w warstwie wyjściowej jest identycznościowa.

Algorytm backprop dla funkcji jednowymiarowych¶

Weźmy architekturę

arch=[1,6,1]

i losowe wagi

weights=func.set_ran_w(arch, 5)

Jak właśnie wspomniano, wartość wyjściowa nie zawiera się teraz w przedziale od 0 do 1, co widać poniżej.

x=func.feed_forward_o(arch, weights,features[1],ff=func.sig,ffo=func.lin)
plt.show(draw.plot_net_w_x(arch, weights,1,x))

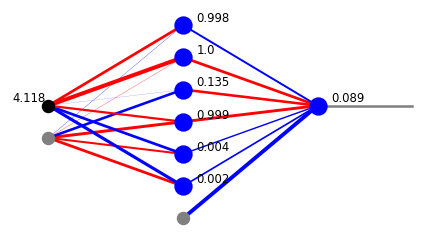
W module biblioteki func mamy funkcję dla algorytmu backprop, która pozwala na zastosowanie jednej funkcji aktywacji w warstwach pośrednich (przyjmujemy sigmoidę) i innej w warstwie wyjściowej (przyjmujemy funkcję identycznościową). Trening jest przeprowadzany w dwóch etapach: w pierwszych 30 rundach pobieramy punkty z próbki treningowej w losowej kolejności, a następnie w kolejnych 1500 rundach przecodzimy kolejno przez wszystkie punkty, zmniejszając również szybkość uczenia eps. Strategia ta jest jedną z wielu możliwych, ale w tym przypadku dobrze spełnia swoje zadanie.

eps=0.02                           # initial learning speed
for k in range(30):                # rounds
    for p in range(len(features)): # loop over the data sample points
        pp=np.random.randint(len(features)) # random point
        func.back_prop_o(features,labels,pp,arch,weights,eps,
                         f=func.sig,df=func.dsig,fo=func.lin,dfo=func.dlin)

for k in range(500):               # rounds
    eps=0.999*eps                  # dicrease of the learning speed
    for p in range(len(features)): # loop over points taken in sequence
        func.back_prop_o(features,labels,p,arch,weights,eps,
                         f=func.sig,df=func.dsig,fo=func.lin,dfo=func.dlin)

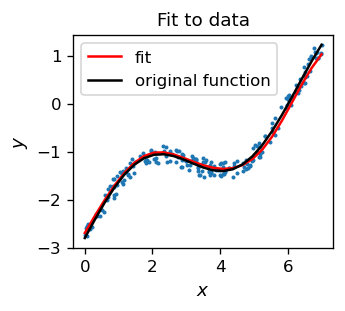
Zauważmy, że otrzymana czerwona krzywa jest bardzo bliska funkcji użytej do wygenerowania próbki danych (czarna linia). Świadczy to o tym, że aproksymacja działa poprawnie. Konstrukcja miary ilościowej (sumy najmniejszych kwadratów) jest tematem ćwiczenia.

Informacja

Funkcja aktywacji w warstwie wyjściowej może być dowolną gładką funkcją o wartościach zawierających wartości interpolowanej funkcji, niekoniecznie liniową.

Więcej wymiarów

Aby interpolować funkcje dwóch lub więcej argumentów, należy użyć sieci ANN z co najmniej trzema warstwami neuronów.

Możemy to rozumieć następująco [MullerRS12]: dwa neurony w pierwszej warstwie neuronowej mogą tworzyć garb we współrzędnej \(x_1\), dwa inne - garb we współrzędnej \(x_2\), i tak dalej dla wszystkich pozostałych wymiarów. Tworząc koniunkcję tych \(n\) garbów w drugiej warstwie neuronów, otrzymujemy funkcję bazową specjalizującą się w obszarze wokół pewnego punktu w wielowymiarowej przestrzeni wejściowej. A zatem odpowiednio duża liczba takich funkcji bazowych może być użyta do aproksymacji w \(n\) wymiarach, w pełnej analogii do przypadku jednowymiarowego.

Wskazówka

Liczba neuronów potrzebnych w procedurze aproksymacji odzwierciedla zachowanie interpolowanej funkcji. Jeśli funkcja ulega licznym znacznym wahaniom, potrzeba więcej neuronów. W jednym wymiarze jest ich zwykle co najmniej dwa razy więcej niż liczba ekstremów funkcji.

Nadmierne dopasowanie (overfitting)

Aby uniknąć tak zwanego problemu nadmiernego dopasowania, danych użytych do aproksymacji musi być znacznie więcej niż parametrów sieci. W przeciwnym razie moglibyśmy dopasować bardzo dokładnie dane treningowe za pomocą funkcji „wahającej się od punktu do punktu”. Jednocześnie, działanie takiej sieci na danych testowych byłoby bardzo kiepskie.

Ćwiczenia¶

\(~\)

Dopasuj punkty danych wygenerowane przez Twoją ulubioną funkcję (jednej zmiennej) z szumem. Pobaw się architekturą sieci i wyciągnij wnioski.
Oblicz sumę kwadratów odległości między wartościami punktów danych treningowych a odpowiadającą im funkcją aproksymującą i wykorzystaj ją jako miarę jakości dopasowania. Sprawdź, jak liczba neuronów w sieci wpływa na wynik.
Użyj sieci o większej liczbie warstw (co najmniej 3 warstwy neuronów) do dopasowania punktów danych wygenerowanych za pomocą ulubionej funkcji dwóch zmiennych. Wykonaj dwuwymiarowe wykresy konturowe dla tej funkcji oraz dla funkcji uzyskanej z sieci neuronowej i porównaj wyniki (oczywiście powinny być podobne, jeśli wszystko działa dobrze).

Sieci neuronowe dla początkujących w Pythonie: wykłady w Jupyter Book

Interpolacja

Zawartość