Wstęp¶

Cel wykładu¶

Celem kursu jest wyłożenie podstaw wszechobecnych sieci neuronowych z pomocą Pythona [Bar16, Gut16, Mat19]. Zarówno kluczowe pojęcia sieci neuronowych, jak i programy ilustrujące są wyjaśniane na bardzo podstawowym poziomie, niemal „licealnym”. Kody, bardzo proste, zostały szczegółowo opisane. Ponadto są utworzone bez użycia specjalistycznych bibliotek wyższego poziomu dla sieci neuronowych, co pomaga w lepszym zrozumieniu przedstawionych algorytmów i pokazuje, jak programować je od podstaw.

Dla kogo jest ta książka?

Czytelnik może być zupełnym nowicjuszem, tylko w niewielkim stopniu zaznajomionym z Pythonem (a właściwie każdym innym językiem programowania) i Jupyterem.

Materiał obejmuje takie klasyczne zagadnienia, jak perceptron i jego najprostsze zastosowania, nadzorowane uczenie z propagacją wsteczną do klasyfikacji danych, uczenie nienadzorowane i klasteryzacja, sieci samoorganizujące się Kohonena oraz sieci Hopfielda ze sprzężeniem zwrotnym. Ma to na celu przygotowanie niezbędnego gruntu dla najnowszych i aktualnych postępów (nie omówionych tutaj) w sieciach neuronowych, takich jak uczenie głębokie, sieci konwolucyjne, sieci rekurencyjne, generatywne sieci przeciwników, uczenie ze wzmacnianiem itp.

W trakcie kursu nowicjuszom zostanie delikatnie przemycone kilka podstawowych programów w Pythonie. W kodach znajdują się objaśnienia i komentarze.

Ćwiczenia

Na końcu każdego rozdziału proponujemy kilka ćwiczeń, których celem jest zapoznanie czytelnika z poruszanymi tematami i kodami. Większość ćwiczeń polega na prostych modyfikacjach/rozszerzeniach odpowiednich fragmentów materiału wykładowego.

Literatura

Podręczników i notatek do wykładów poświęconych zagadnieniom poruszanym na tym kursie jest niezliczona ilość, stąd autor nie będzie próbował przedstawiać nawet niepełnego spisu literatury. Przytaczamy tylko pozycje, na które może spojrzeć bardziej zainteresowany czytelnik.

Z prostotą jako drogowskazem, wybór tematów był inspirowany szczegółowymi wykładami Daniela Kerstena w programie Mathematica, z internetowej książki Raula Rojasa (dostępna również w wersji drukowanej [FR13]) oraz z punktu widzenia fizyków (jak ja!) z [MullerRS12].

Inspiracja biologiczna¶

Inspiracją do opracowania matematycznych modeli obliczeniowych omawianych w tym kursie jest struktura biologiczna naszego układu nerwowego [KSJ+12]. Centralny układ nerwowy (mózg) zawiera ogromną liczbę ($\sim 10^{11}$) neuronów, które można postrzegać jako maleńkie elementarne procesory. Otrzymują one sygnał poprzez dendryty, a jeśli jest on wystarczająco silny, jądro decyduje (obliczenie jest wykonane tutaj!) „wystrzelić” sygnał wyjściowy wzdłuż aksonu, gdzie jest on następnie przekazywany przez zakończenia aksonów do dendrytów innych neuronów. Połączenia aksonowo-dendryczne (połączenia synaptyczne) mogą być słabe lub silne, modyfikując przekazywany bodziec. Co więcej, siła połączeń synaptycznych może się zmieniać w czasie (reguła Hebba mówi nam, że połączenia stają się silniejsze, jeśli są używane wielokrotnie). W tym sensie neuron jest „programowalny”.

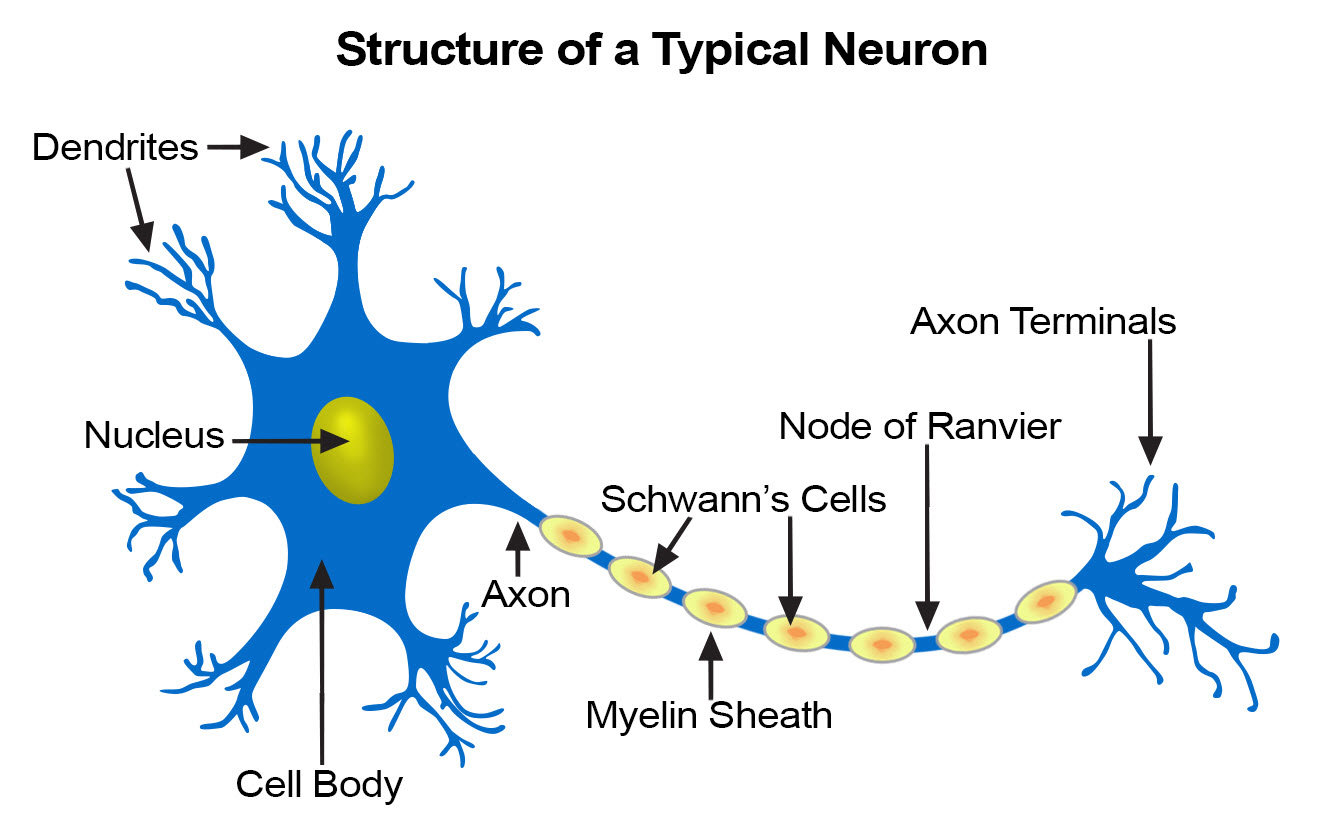
Rys. 1 Biologiczny neuron (https://training.seer.cancer.gov/anatomy/nervous/tissue.html).¶

Możemy zadać sobie pytanie, czy liczbę neuronów w mózgu rzeczywiście należy określać jako tak „ogromną”, jak się zwykle twierdzi. Porównajmy to do urządzeń obliczeniowych z układami pamięci. Liczba neuronów 10$^{11}$ z grubsza odpowiada liczbie tranzystorów w chipie pamięci o pojemności 10 GB, co nie robi na nas specjalnego wrażenia, skoro w dzisiejszych czasach możemy kupić takie urządzenie za około 2$.

Co więcej, prędkość przemieszczania się impulsów nerwowych, która jest wynikiem procesów elektrochemicznych, również nie jest imponująca. Najszybsze sygnały, takie jak te związane z pobudzaniem mięśni, przemieszczają się z prędkością do 120 m/s (osłonki mielinowe są niezbędne do ich osiągnięcia). Sygnały dotykowe osiągają około 80m/s, podczas gdy ból jest przenoszony ze stosunkowo bardzo małymi prędkościami 0,6m/s. To dlatego kiedy upuszczasz młotek na palec u nogi, czujesz to natychmiast, ale ból dociera do mózgu z opóźnieniem ~1s, ponieważ musi pokonać odległość ~1,5m. Z drugiej strony, w urządzeniach elektronicznych sygnał przemieszcza się w przewodach z prędkością rzędu prędkości światła, $\sim 300000{\rm km/s}=3\times 10^{8}{\rm m/ s}$!

W przypadku ludzi średni czas reakcji wynosi 0,25 s na bodziec wizualny, 0,17 s na bodziec dźwiękowy i 0,15 s na dotyk. W ten sposób ustawienie progowego czasu dla falstartu w sprintach na 0,1 s jest bezpiecznie poniżej możliwej reakcji biegacza. Są to niezwykle powolne reakcje w porównaniu z odpowiedziami elektronicznymi.

Na podstawie zużycia energii przez mózg można oszacować, że neuron kory mózgowej odpala średnio raz na 6 sekund. Jest też mało prawdopodobne, aby przeciętny neuron odpalał częściej niż raz na sekundę. Pomnożenie tej szybkości wyzwalania przez liczbę wszystkich neuronów korowych, $\sim 1.6 \times 10^{10}$, daje około 3 $\times 10^{9}$ wyładowań/s w korze, czyli 3GHz. To jest cżęstotliwość This aktowania typowego chipa procesora! Jeśli więc odpalanie neuronu utożsamić z elementarnym obliczeniem, to tak określona moc mózgu jest z grubsza porównywalna z mocą standardowego procesora komputerowego.

Powyższe fakty wskazują, że z punktu widzenia naiwnych porównań z chipami krzemowymi ludzki mózg nie jest niczym szczególnym. Co zatem daje nam nasze wyjątkowe zdolności: niesłychanie wydajne rozpoznawanie wzorców wizualnych i dźwiękowych, myślenie, świadomość, intuicję, wyobraźnię? Odpowiedź wiąże się z niesamowicie rozbudowaną architekturą mózgu, w której każdy neuron (jednostka procesora) jest połączony poprzez synapsy średnio aż z 10000 (!) innych neuronów. Ta cecha sprawia, że jest ona radykalnie inna i znacznie bardziej skomplikowana niż architektura składająca się z jednostki sterującej, procesora i pamięci w naszych komputerach (architektura maszyny von Neumanna) . Tam liczba połączeń jest rzędu liczby bitów pamięci, natomiast w ludzkim mózgu jest około $10^{15}$ połączeń synaptycznych. Jak wspomniano, połączenia można „zaprogramować”, aby były silniejsze lub słabsze. Jeśli, dla prostego oszacowania, przybliżylibyśmy siłę połączenia tylko przez dwa stany synapsy, 0 lub 1, to całkowita liczba konfiguracji kombinatorycznych takiego systemu wynosiłaby $2^{10^{15}}$ - „hiper-ogromna” liczba. Większość takich konfiguracji, oczywiście, nigdy nie jest realizowana w praktyce, niemniej jednak liczba możliwych stanów konfiguracyjnych mózgu lub „programów”, które może on realizować, jest naprawdę ogromna.

W ostatnich latach, wraz z rozwojem potężnych technik obrazowania, możliwe stało się mapowanie połączeń w mózgu z niespotykaną dotąd rozdzielczością, gdzie widoczne są pojedyncze wiązki nerwów. Wysiłki te są częścią [Projektu Human Connectome] (http://www.humanconnectomeproject.org), którego ostatecznym celem jest dokłdne odwzorowanie architektury ludzkiego mózgu. W przypadku znacznie prostszej muszki owocowej, projekt drosophila connectome jest bardzo zaawansowany.

Rys. 2 Architektura mózgu włókna istoty białej (z projektu Human Connectome humanconnectomeproject.org)¶

Ważne

Cecha „ogromnej łączności”, z miriadami neuronów służących jako równoległe procesory elementarne, sprawia, że mózg jest zupełnie innym urządzeniem obliczeniowym niż maszyna von Neumanna (tj. nasze codzienne komputery).

Sieci feed-forward¶

Neurofizjologiczne badania mózgu dostarczają ważnych wskazówek dla modeli matematycznych stosowanych w sztucznych sieciach neuronowych (ANN). I odwrotnie, postępy w algorytmice ANN często przybliżają nas do zrozumienia, jak faktycznie może działać nasz „komputer mózgowy”!

Najprostsze sieci ANN to tak zwane sieci feed forward, zilustrowane w Rys. 3. Składają się one z warstwy wejściowej (czarne kropki), która reprezentuje tylko dane cyfrowe, oraz warstw neuronów (kolorowych kropek). Liczba neuronów w każdej warstwie może być różna. Złożoność sieci i zadań, które może ona realizować, rośnie rzecz jasna wraz z liczbą warstw i liczbą neuronów.

W dalszej części tego rozdziału podamy, w dość skondensownej postaci, kilka ważnych definicji:

Sieci z jedną warstwą neuronów nazywane są sieciami jednowarstwowymi. Ostatnia warstwa (jasnoniebieskie kropki) nazywana jest warstwą wyjściową. W sieciach wielowarstwowych (więcej niż jedna warstwa neuronowa) warstwy neuronowe poprzedzające warstwę wyjściową (fioletowe kropki) nazywane są warstwami pośrednimi. Jeśli liczba warstw jest duża (np. 64, 128, …), mamy do czynienia ze stosowanymi od niedawna „przełomowymi” głębokimi sieciami.

Neurony w różnych warstwach nie muszą działać w ten sam sposób, w szczególności neurony wyjściowe mogą zachowywać się inaczej niż pośrednie.

Sygnał z wejścia wędruje po wskazanych strzałkami łączach (krawędziach, połączeniach synaptycznych) do neuronów w kolejnych warstwach. W sieciach typu feed-forward, jak ta na Rys. 3, sygnał może poruszać się tylko do przodu (na rysunku od lewej do prawej): od wejścia do pierwszej warstwy neuronowej, od pierwszej do drugiej, i tak dalej, aż do osiągnięcia wyjścia. Nie jest dozwolone cofanie się do poprzednich warstw ani równoległa propagacja pomiędzy neuronami tej samej warstwy. Byłaby to wówczas sieć z powracaniem, o czym nieco mówimy w rozdziale Lateral inhibition.

Jak szczegółowo opisujemy w kolejnych rozdziałach, wędrujący sygnał jest odpowiednio przetwarzany przez neurony, stąd urządzenie wykonuje obliczenia: wejście jest przekształcane w wyjście.

W przykładowej sieci Rys. 3 każdy neuron z poprzedniej warstwy jest połączony z każdym neuronem w następnej warstwie. Takie sieci ANN są nazywane w pełni połączonymi.

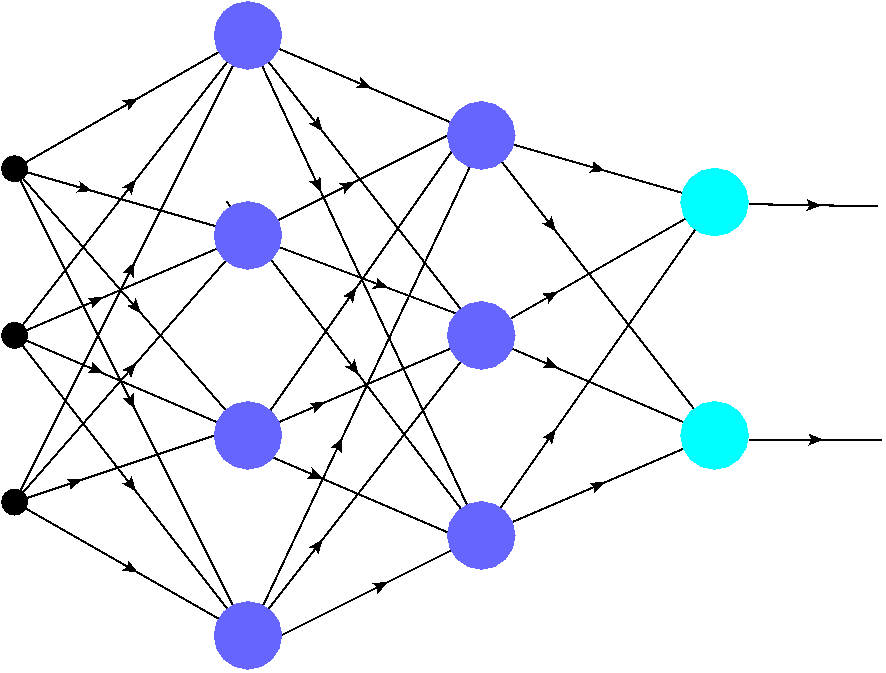
Rys. 3 Przykładowa, w pełni połączona sztuczna sieć neuronowa typu feed-forward. Kolorowe plamy reprezentują neurony, a krawędzie uskazują połączenia synaptyczne. Sygnał rozchodzi się od wejścia (czarne kropki), przez neurony w kolejnych warstwach pośrednich (ukrytych) (fioletowe kropki), do warstwy wyjściowej (jasnoniebieskie kropki). Siła połączeń jest kontrolowana przez wagi (hiperparametry) przypisane do krawędzi.¶

Jak omówimy bardziej szczegółowo późniwj, każda krawędź (połączenie synaptyczne) w sieci ma pewną „siłę” opisaną liczbą o nazwie waga (wagi są również określane jako hiperparametry). Nawet bardzo małe w pełni połączone sieci, takie jak ta z Rys. 3, mają bardzo wiele połączeń (tutaj 30), stąd zawierają dużo hiperparametrów. Tak więc, choć czasami wyglądają niewinnie, ANN są w rzeczywistości bardzo złożonymi systemami wieloparametrycznymi. Co więcej, kluczową cechą jest tutaj nieliniowość odpowiedzi neuronów, co omawiamy w kolejnym rozdziale Neuron MCP.

Dlaczego Python¶

Wybór języka Python dla prościutkich kodów tego kursu prawie nie wymaga wyjaśnienia. Zacytujmy tylko Tima Petersa:

Piękne jest lepsze niż brzydkie.
Jawne jest lepsze niż niejawne.
Proste jest lepsze niż złożone.
Złożone jest lepsze niż skomplikowane.
Liczy się czytelność.

Według SlashData, na świecie jest obecnie ponad 10 milionów programistów używających Pythona, zaraz po jezyku JavaScript (~14 milionów). W szczególności Python okazuje się bardzo praktyczny w zastosowaniach do sieci ANN.

Importowane pakiety¶

W trakcie tego kursu używamy kilku standardowych pakietów bibliotecznych Pythona do obliczeń numerycznych, wykresów itp. Jak podkreśliliśmy, nie korzystamy z żadnych bibliotek specjalnie dedykowanych sieciom neuronowym. Notebook każdego wykładu zaczyna się od zaimportowania niektórych z tych bibliotek:

import numpy as np              # numerical
import statistics as st         # statistics
import matplotlib.pyplot as plt # plotting
import matplotlib as mpl        # plotting
import matplotlib.cm as cm      # contour plots 

from mpl_toolkits.mplot3d.axes3d import Axes3D   # 3D plots
from IPython.display import display, Image, HTML # display imported graphics

neural package

Tworzone podczas tego kursu funkcje, które są później wielokrotnie używane, są umieszczane w pakiecie prywatnej biblioteki neural, opisanym w załączniku Pakiet neural.

Celem kompatybilności z środowikiem Google Colab, pakiet neural importowany jest z repozytorium w następujący sposób:

import os.path 

isdir = os.path.isdir('lib_nn') # check whether 'lib_nn' exists

if not isdir:
   !git clone https://github.com/bronwojtek/lib_nn.git # cloning the library from github

import sys                     
sys.path.append('./lib_nn') 

from neural import *            # importing my library package

Więcej informacji można znaleźć w dodatku Pakiet neural.

Informacja

Dla zwięzłości prezentacji, niektóre zbędne (np. import bibliotek) lub nieistotne fragmenty kodu są obecne tylko w notebookach Jupytera (do pobrania) i nie są ukazywane w książce. Dzięki temu tekst jest krótszy i czytelny.

Sieci neuronowe dla początkujących w Pythonie: wykłady w Jupyter Book

Wstęp

Zawartość