Rektyfikacja
Zawartość
Rektyfikacja¶
W poprzednim rozdziale utworzyliśmy z dwóch sigmoidów funkcję o kształcie garbu, która, jak pokazaliśmy, mogła stanowić funkcję bazową dla aproksymacji. Możemy teraz zadać nastepujące pytanie: czy możemy skonstruować sam sigmoid jako kombinację liniową (różnicę) pewych innych funkcji? Wtedy moglibyśmy użyć tychże funkcji do aktywacji neuronów zamiast sigmoidu. Odpowiedź brzmi tak. Na przykład funkcja Rectified Linear Unit (ReLU)
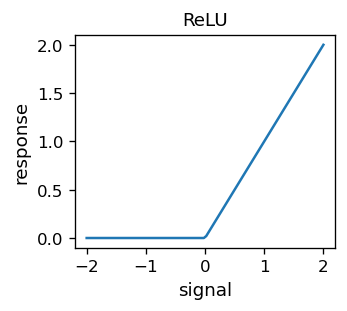
wykonuje (w przybliżeniu) to zadanie. Ta nieco niezręczna nazwa pochodzi z elektrotechniki (rektyfikacja oznacza prostowanie), w której prostownik służy do odcinania ujemnych wartości sygnału elektrycznego. Wykres funkcji ReLU wygląda następująco:
Różnica dwóch funkcji ReLU o przesuniętych argumentach daje przykładowy wynik
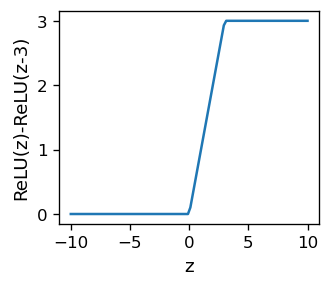
która jakościowo wygląda jak sigmoid, z wyjątkiem ostrych rogów. Aby uzyskać gładkość, można skorzystać z innej funkcji - softplus,
która ma nastepujący wykres:
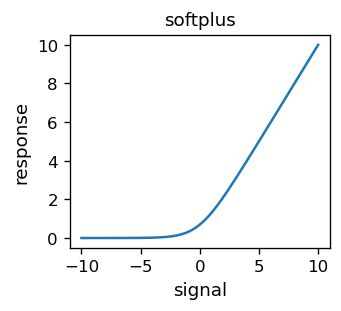
Różnica dwóch funkcji softplus o przesuniętym argumencie daje wynik bardzo podobny do sigmoidu:
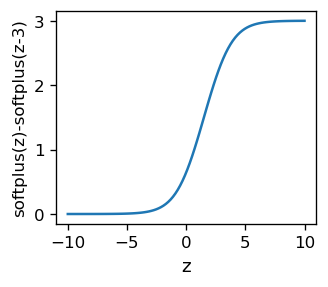
Informacja
Do aktywacji można użyć ReLU, softplus lub wielu innych podobnych funkcji.
Dlaczego właściwie należy to robić, zostanie omówione później.
Interpolacja z ReLU¶
Nasze symulowane dane możemy aproksymować za pomocą sieci ANN z aktywacją ReLU w warstwach pośrednich (w warstwie wyjściowej funcja aktywacji jest identycznościowa, tak jak w poprzednim rozdziale). W poniższych kodach funkcje zostały zaczerpnięte z modułu func.
#fff=func.softplus # short-hand notation
#dfff=func.dsoftplus
fff=func.relu # short-hand notation
dfff=func.drelu
Sieć musi mieć teraz więcej neuronów, ponieważ sigmoid „rozpada się” na dwie funkcje ReLU:
arch=[1,30,1] # architecture
weights=func.set_ran_w(arch, 5) # initialize weights randomly in [-2.5,2.5]
Symulacje przeprowadzamy dokładnie tak samo jak w poprzednim przypadku. Doświadczenie mówi, że należy startować z małymi szybkościami uczenia się. Dwa zestawy rund (podobnie jak w poprzednim rozdziale)
eps=0.0003 # small learning speed
for k in range(30): # rounds
for p in range(len(features)): # loop over the data sample points
pp=np.random.randint(len(features)) # random point
func.back_prop_o(features,labels,pp,arch,weights,eps,
f=fff,df=dfff,fo=func.lin,dfo=func.dlin) # teaching
for k in range(3000): # rounds
# eps=eps*.995
if k%100==99: print(k+1,' ',end='') # print progress
for p in range(len(features)): # points in sequence
func.back_prop_o(features,labels,p,arch,weights,eps,
f=fff,df=dfff,fo=func.lin,dfo=func.dlin) # teaching
100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100 2200 2300 2400 2500 2600 2700 2800 2900 3000
for k in range(3000): # rounds
eps=eps*.995
if k%100==99: print(k+1,' ',end='') # print progress
for p in range(len(features)): # points in sequence
func.back_prop_o(features,labels,p,arch,weights,eps,
f=fff,df=dfff,fo=func.lin,dfo=func.dlin) # teaching
100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100 2200 2300 2400 2500 2600 2700 2800 2900 3000
dają wynik
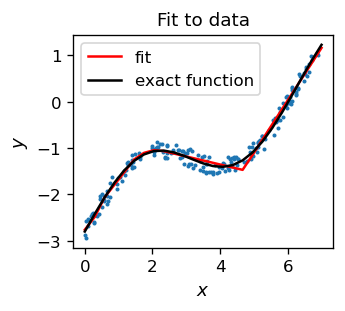
Ponownie uzyskujemy całkiem zadowalający wynik (linia czerwona), zauważając, że wykres funkcji dopasowania jest ciągiem linii prostych, co odzwierciedla właściwości użytej funkcji aktywacji ReLU. Gładki wynik można uzyskać z pomocą funkcji softplus.
Klasyfikatory z rektyfikacją¶
Istnieją techniczne powody przemawiające za stosowaniem w algorytmie backprop funkcji rektyfikowanych zamiast sigmoidalnych. Pochodne sigmoidu są bowiem bardzo bliskie zera, z wyjątkiem wąskiego obszaru w pobliżu progu. Sprawia to, że aktualizacja wag jest mało prawdopodobna, zwłaszcza gdy cofamy się o wiele warstw wstecz, ponieważ wtedy bardzo małe liczby (określone przez pochodne funkcji) są przemnażane i w zasadzie nie prowadzą do żadnej aktualizacji (zjawsko to jest znane jako problem zanikającego gradientu). W przypadku funkcji rektyfikowanych zakres, w którym pochodna jest istotnie różna od zera, jest duży (w przypadku ReLU dotyczy to wszystkich współrzędnych dodatnich), dlatego problem zanikającego gradientu się nie pojawia. Właśnie z tego powodu funkcje rektyfikowane są stosowane w głębokich sieciach ANN, w których jest wiele warstw, niemożliwych do wytrenowania przy funkcjach aktywacji jest typu sigmoidalnego.
Informacja
Zastosowanie rektyfikowanych funkcji aktywacji było jednym z kluczowych trików, które umożliwiły przełom w rozwoju głębokich ANN około 2011 roku.
Z drugiej strony, w przypadku ReLU może się zdarzyć, że niektóre wagi przyjmą takie wartości, że wiele neuronów stanie się nieaktywnych, tzn. nigdy, dla żadnego inputu, nie zadziałają – zostaną de facto wyeliminowane. Nazywa się to problemem „martwego neuronu” lub „trupa”, który pojawia się zwłaszcza wtedy, gdy parametr szybkości uczenia jest zbyt duży. Sposobem na ograniczenie tego problemu jest zastosowanie funkcji aktywacji, która w ogóle nie ma przedziału o zerowej pochodnej, np. Leaky ReLU. Tutaj przyjmiemy jej nasepującą postać
Dla ilustracji powtórzymy nasz przykład z rozdz. Przykład z kołem z klasyfikacją punktów w kole z wykorzystaniem funkcji Leaky ReLU.
Przyjmujemy następującą architekturę i parametry początkowe:
arch_c=[2,20,1] # architecture
weights=func.set_ran_w(arch_c,3) # scaled random initial weights in [-1.5,1.5]
eps=.01 # initial learning speed
i uruchamiamy algorytm w dwóch etapach: z Leaky ReLU, a następnie z ReLU:
for k in range(300): # rounds
eps=.999*eps # decrease the learning speed
if k%100==99: print(k+1,' ',end='') # print progress
for p in range(len(features_c)): # loop over points
func.back_prop_o(features_c,labels_c,p,arch_c,weights,eps,
f=func.lrelu,df=func.dlrelu,fo=func.sig,dfo=func.dsig)
# backprop with leaky ReLU
100 200 300
for k in range(700): # rounds
eps=.995*eps # decrease the learning speed
if k%100==99: print(k+1,' ',end='') # print progress
for p in range(len(features_c)): # loop over points
func.back_prop_o(features_c,labels_c,p,arch_c,weights,eps,
f=func.relu,df=func.drelu,fo=func.sig,dfo=func.dsig)
# backprop with ReLU
100 200 300 400 500 600 700
Wynik jest całkiem zadowalający, co pokazuje, że metoda działa. Przy obecnej architekturze i funkcjach aktywacji, co nie jest zaskakujące, na poniższym wykresie można zauważyć ślady wielokąta przybliżającego koło.
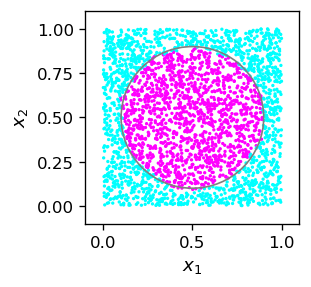
Ćwiczenia¶
\(~\)
Zastosuj różne rektywikowane funkcje aktywacji dla klasyfikatorów binarnych i przetestuj je na różnych kształtach (analogicznie do przykładu z kołem powyżej).
Przekonaj się, że uruchomienie algorytmu backprop (z funkcją ReLU) ze zbyt dużą początkową szybkością uczenia prowadzi do problemu „martwego neuronu” i niepowodzenia algorytmu.