Więcej warstw
Zawartość
Więcej warstw¶
Dwie warstwy neuronów¶
W poprzednim rozdziale pokazaliśmy, że neuron MCP ze schodkową funkcją aktywacji odpowiada nierówności \(x \cdot w=w_0+x_1 w_1 + \dots x_n w_n > 0\), gdzie \(n\) jest wymiarem przestrzeni wejściowej. Pouczające jest dalsze prześledzenie tej geometrycznej interpretacji. Przyjmując dla prostoty \(n=2\) (płaszczyzna), powyższa nierówność odpowiada jej podziałowi na dwie półpłaszczyzny. Jak wiemy, prosta wyrażona jest równaniem
i stanowi linię podziału na dwie półpłaszczyzny.
Wyobraźmy sobie teraz, że mamy więcej takich warunków: dwa, trzy itd., ogólnie \(k\) niezależnych warunków. Biorąc koniunkcję tych warunków, możemy zbudować wypukłe obszary, jak przykładowo pokazano na Rys. 7.
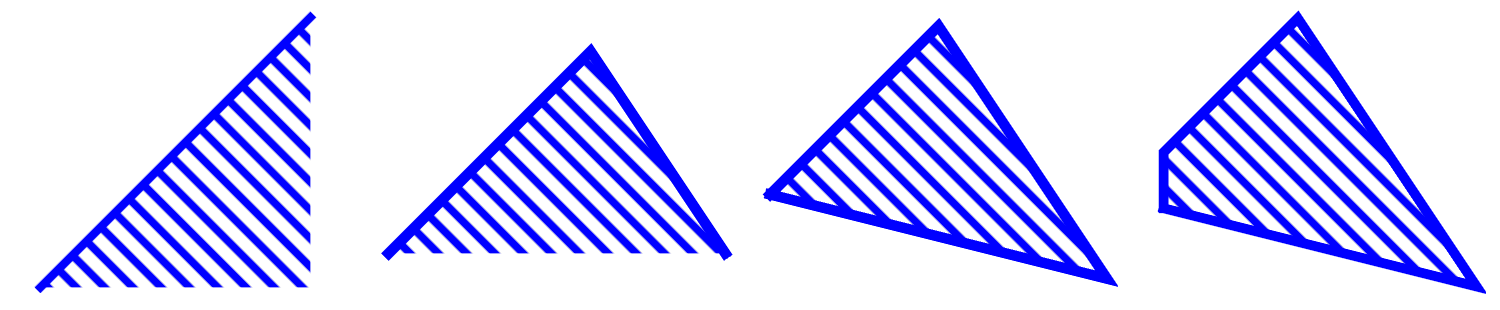
Rys. 7 Przykładowe obszary wypukłe na płaszczyźnie, od lewej do prawej: z jednym warunkiem nierówności, z koniunkcjami 2 warunków i z koniukcjami 3 lub 4 warunków nierówności, dającymi wielokąty.¶
Obszar wypukły
Z definicji obszar \(A\) jest wypukły wtedy i tylko wtedy, gdy odcinek pomiędzy dowolnymi dwoma punktami w \(A\) jest zawarty w \(A\). Obszar, który nie jest wypukły nazywa się wklęsłym.
Oczywiście, \(k\) warunków nierówności można narzucić za pomocą \(k\) neuronów MCP. Przypomnijmy sobie z rozdz. Funkcje logiczne, że możemy w prosty sposób budować funkcje logiczne za pomocą sieci neuronowych. W szczególności możemy dokonać koniunkcji \(k\) warunków, biorąc neuron o wagach \(w_0=-1\) i \(1/k < w_i < 1/(k-1)\), gdzie \(i=1,\dots ,k\). Jedną z możliwości jest np.
Rzeczywiście, niech \(p_0=1\), a warunki narzucone przez nierówności oznaczymy jako \(p_i\), \(i=1,\dots,k\), które mogą przyjmować wartości 1 lub 0 (prawda lub fałsz). Następnie
wtedy i tylko wtedy, gdy wszystkie \(p_i=1\), tj. wszystkie warunki są spełnione.
Architektury sieci dla warunków \(k=1\), 2, 3 lub 4 są ukazane na Rys. 8. Idąc od lewej do prawej począwszy od drugiego panelu, mamy sieci z dwiema warstwami neuronów i z \(k\) neuronami w warstwie pośredniej, zapewniającymi warunki nierówności, oraz jednym neuronem w warstwie wyjściowej, pełniącym funkcję bramki AND. Oczywiście dla jednego warunku wystarczy mieć jeden neuron, jak pokazano na lewym panelu Rys. 8.
W interpretacji geometrycznej pierwsza warstwa neuronowa reprezentuje \(k\) półpłaszczyzn, a neuron w drugiej warstwie odpowiada obszarowi wypukłemu o \(k\) bokach.
Sytuacja w oczywisty sposób uogólnia się na dane w większej liczbie wymiarów. W takim przypadku mamy więcej czarnych kropek dla danych wejściowych na Rys. 8. Geometrycznie dla \(n=3\) mamy do czynienia z dzieleniem na półprzestrzenie z pomocą płaszczyzn i tworzenie wypukłych wielościanów, a dla \(n>3\) z dzieleniem hiperprzestzreni [hiperpłaszczyznami](https:/ /en.wikipedia.org/wiki/Hyperplane) i tworzeniem wypukłych politopów.
Informacja
Jeśli w warstwie pośredniej znajduje się wiele neuronów, powstały wielokąt ma wiele boków, które mogą przybliżać gładką granicę, taką jak łuk. Aproksymacja jest coraz lepsza w miarę wzrostu \(k\).
Ważne
Percepton z dwiema warstwami neuronów (z wystarczającą liczbą neuronów w warstwie pośredniej) może klasyfikować punkty należące do obszaru wypukłego w przestrzeni \(n\)-wymiarowej.
Trzy lub więcej warstw neuronów¶
Pokazaliśmy właśnie, że sieć dwuwarstwowa może klasyfikować wielokąt wypukły. Wyobraźmy sobie teraz, że tworzymy dwie takie figury w drugiej warstwie neuronów, na przykład dzieki następującej sieci:
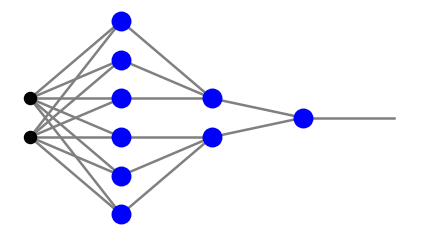
Zauważmy, że pierwsza i druga warstwa neuronów nie są tutaj w pełni połączone, ponieważ „układamy na sobie” dwie sieci tworzące trójkąty, jak w trzecim panelu Rys. 8. Następnie w trzeciej warstwie neuronowej (tutaj posiadającej pojedynczy neuron) implementujemy bramkę \(p \,\wedge \!\sim\!q\), czyli koniunkcję warunków, że punkty należą do jednego trójkąta, a nie należą do drugiego. Jak zaraz pokażemy, przy odpowiednich wagach powyższa siatka może wytworzyć obszar wklęsły, na przykład trójkąt z trójkątnym wgłębieniem:

Rys. 9 Trójkąt z trójkątnym wgłębieniem.¶
Uogólniając ten argument na inne kształty, można pokazać ważne twierdzenie:
Ważne
Perceptron z trzema lub więcej warstwami neuronów (z wystarczającą liczbą neuronów w warstwach pośrednich) może klasyfikować punkty należące do dowolnego regionu w \(n\)-wymiarowej przestrzeni z \(n-1\)-wymiarowymi ograniczeniami przez hiperpłaszczyzny.
Informacja
Warto tutaj podkreślić, że trzy warstwy zapewniają pełną funkcjonalność! Dodawanie kolejnych warstw do klasyfikatora nie zwiększa jego możliwości.
Feed forward w Pythonie¶
Zanim przejdziemy do przykładu, potrzebujemy kodu w Pythonie do propagacji sygnału w przód w ogólnej, w pełni połączonej sieci. Będziemy reprezentować architekturę sieci z \(l\) warstwami neuronów jako tablicę postaci
gdzie \(n_0\) jest liczbą węzłów wejściowych, a \(n_i\) liczbą neuronów w warstwach \(i=1,\dots,l\). Na przykład architektura sieci z czwartego panelu Rys. 8 to
arch=[2,4,1]
arch
[2, 4, 1]
W kodach tego kursu posługujemy się konwencją z Rys. 5, a mianowicie próg jest traktowany jednolicie z pozostałym sygnałem. Jednak węzły progowe nie są uwzględniane w określaniu liczb \(n_i\) zdefiniowanych powyżej. W szczególności bardziej szczegółowy widok czwartego panelu Rys. 8 to
plt.show(draw.plot_net(arch))
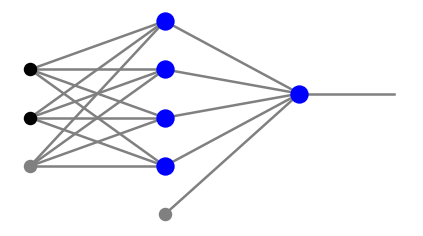
Czarne kropki oznaczają dane wejściowe, szare kropki odpowiadają węzłom progowym, dającym input równy 1, a niebieskie kółka to neurony.
Następnie potrzebujemy wagi połączeń. Mamy \(l\) zestawów wag, z których każdy odpowiada krawędziom wchodzącym do danej warstwy neuronowej od lewej strony. W powyższym przykładzie pierwsza warstwa neuronów (niebieskie kółka po lewej stronie) ma wagi, które tworzą macierz \(3 \times 4\). Tutaj 3 to liczba węzłów w poprzedniej (wejściowej) warstwie (łącznie z węzłem progowym), a 4 to liczba neuronów w pierwszej warstwie neuronowej. Podobnie wagi związane z drugą (wyjściową) warstwą neuronową tworzą macierz \(4 \times 1\). Stąd w naszej konwencji macierze wag odpowiadające kolejnym warstwom neuronów \(1, 2, \dots, l\) mają wymiary
Tak więc, aby przechowywać wszystkie wagi sieci, tak naprawdę potrzebujemy trzech wskaźników: jeden dla warstwy, jeden dla liczby węzłów w poprzedniej warstwie i jeden dla liczby węzłów w danej warstwie. Moglibyśmy tutaj użyć trójwymiarowej tablicy, ale ponieważ numerujemy warstwy neuronów zaczynając od 1, a tablice zaczynają się od 0, nieco wygodniej jest użyć struktury słownika Pythona. Przechowujemy zatem wagi jako
gdzie \(arr^i\) jest dwuwymiarową tablicą (macierzą) wag dla warstwy neuronowej \(i\). Dla przypadku z powyższego rysunku możemy wziąć na przykład
w={1:np.array([[1,2,1,1],[2,-3,0.2,2],[-3,-3,5,7]]),2:np.array([[1],[0.2],[2],[2],[-0.5]])}
print(w[1])
print("")
print(w[2])
[[ 1. 2. 1. 1. ]
[ 2. -3. 0.2 2. ]
[-3. -3. 5. 7. ]]
[[ 1. ]
[ 0.2]
[ 2. ]
[ 2. ]
[-0.5]]
Dla sygnału rozchodzącego się w sieci stosujemy również odpowiednio słownik w postaci
gdzie \(x^0\) to wejście, a \(x^i\) to sygnał wychodzący z warstwy neuronowej \(i\), dla \(i=1, \dots, l\). Wszystkie symbole \(x^j\), \(j=0, \dots, l\) są tablicami jednowymiarowymi. Uwzględniamy tu węzły progowe, stąd wymiary \(x^j\) wynoszą \(n_j+1\), z wyjątkiem warstwy wyjściowej, która nie ma węzła odchylenia, stąd \(x^l\) ma wymiar \(n_l\). Innymi słowy, wymiary tablic sygnału są równe całkowitej liczbie węzłów w każdej warstwie.
Następnie przedstawiamy szczegółowo odpowiednie wzory, ponieważ jest to kluczowe dla uniknięcia ewentualnych pomyłek związanych z zapisem. Wiemy już z (2), że dla pojedynczego neuronu z \(n\) wejściami, sygnał wchodzący jest obliczany jako
Przy większej liczbie warstw (oznaczonych wskażnikiem górnym \(i\)) i liczbie neuronów \(n_i\) w warstwie \(i\), notacja uogólnia się na
Zauważmy, że sumowanie zaczyna się od \(\beta=0\), aby uwzględnić węzeł progowy w poprzedniej warstwie \((i-1)\), ale \(\alpha\) zaczyna się od 1, ponieważ tylko neurony (a nie węzeł progowy) w warstwie \(i\) odbierają sygnał (patrz rysunek poniżej).
W notacji macierzowej możemy też zapisać bardziej zwięźle \(s^{iT} = x^{(i-1)T} W^i\), gdzie \(T\) oznacza transpozycję, tzn.
Jak już dobrze wiemy, wyjście z neuronu uzyskuje się działając na jego sygnał wejściowy funkcją aktywacji. W ten sposób w końcu mamy
z węzłami progowymi równymi jeden. Poniższy rysunek ilustruje naszą notację.
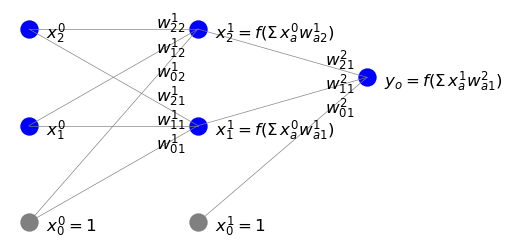
Implementacja propagacji feed-forward w Pythonie jest następująca:
def feed_forward(ar, we, x_in, f=func.step):
"""
Feed-forward propagation
input:
ar - array of numbers of nodes in subsequent layers [n_0, n_1,...,n_l]
(from input layer 0 to output layer l, bias nodes not counted)
we - dictionary of weights for neuron layers 1, 2,...,l in the format
{1: array[n_0+1,n_1],...,l: array[n_(l-1)+1,n_l]}
x_in - input vector of length n_0 (bias not included)
f - activation function (default: step)
return:
x - dictionary of signals leaving subsequent layers in the format
{0: array[n_0+1],...,l-1: array[n_(l-1)+1], l: array[nl]}
(the output layer carries no bias)
"""
l=len(ar)-1 # number of the neuron layers
x_in=np.insert(x_in,0,1) # input, with the bias node inserted
x={} # empty dictionary x
x.update({0: np.array(x_in)}) # add input signal to x
for i in range(1,l): # loop over layers except the last one
s=np.dot(x[i-1],we[i]) # signal, matrix multiplication
y=[f(s[k]) for k in range(arch[i])] # output from activation
x.update({i: np.insert(y,0,1)}) # add bias node and update x
# the output layer l - no adding of the bias node
s=np.dot(x[l-1],we[l]) # signal
y=[f(s[q]) for q in range(arch[l])] # output
x.update({l: y}) # update x
return x
Dla zwięzłości przyjmujemy konwencję, w której nie przekazujemy w argumentach funkcji węzła progowego. Jest on wstawiany do funkcji za pomocą np.insert(x_in,0,1). Jak zwykle używamy np.dot do mnożenia macierzy.
Następnie testujemy, jak feed_forward działa dla przykładowych danych wejściowych.
xi=[2,-1]
x=func.feed_forward(arch,w,xi,func.step)
print(x)
{0: array([ 1, 2, -1]), 1: array([1, 1, 0, 0, 0]), 2: [1]}
Końcowy output z tej sieci jest uzyskany jako
x[2][0]
1
Dygresja o sieciach liniowych¶
Zróbmy teraz następującą obserwację. Załóżmy, że mamy sieć z liniową funkcją aktywacji \(f(s)=c s\). Wtedy ostatnia formuła z powyższego wyprowadzenia przyjmuje postać
lub w notacji macierzowej:
Powtarzając to, otrzymujemy sygnał w warstwie wyjściowej
gdzie \(W=c^l w^1 w^2 \dots w^l\). Widzimy wiec, że taka sieć jest równoważna sieci jednowarstwowej z macierzą wag \(W\) określoną powyżej.
Informacja
Z tego powodu nie ma sensu rozważanie sieci wielowarstwowych z liniową funkcją aktywacji.
Wizualizacja¶
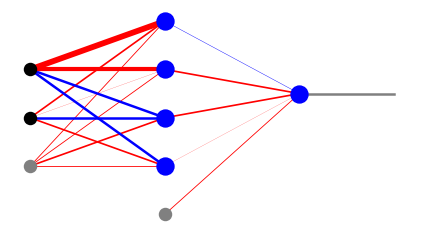
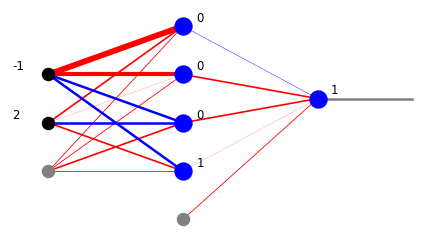
W celu wizualizacji prostych sieci w module draw pakietu neural udostępniamy kilka funkcji rysowania, które ukazują zarówno wagi, jak i sygnały w sieci. Funkcja plot_net_w rysuje wagi dodatnie na czerwono, a ujemne na niebiesko, przy czym szerokości odzwierciedlają ich wielkość. Ostatni parametr, tutaj 0.5, przeskalowuje szerokości tak, że grafika wygląda ładnie. Funkcja plot_net_w_x drukuje dodatkowo wartości sygnału wychodzącego z węzłów każdej warstwy.
plt.show(draw.plot_net_w(arch,w,0.5))
plt.show(draw.plot_net_w_x(arch,w,0.5,x))
Klasyfikator z trzema warstwami neuronów¶
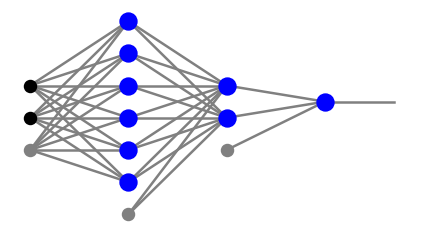
Jesteśmy teraz gotowi do jawnego skonstruowania przykładu binarnego klasyfikatora punktów w obszarze wklęsłym: trójkąta z trójkątnym wycięciem z Rys. 9. Architektura sieci to
arch=[2,6,2,1]
plt.show(draw.plot_net(arch))
Warunki geometryczne i odpowiadające im wagi dla pierwszej warstwy neuronowej to
\(\alpha\) |
warunek |
\(w_{0\alpha}^1\) |
\(w_{1\alpha}^1\) |
\(w_{2\alpha}^1\) |
|---|---|---|---|---|
1 |
\(x_1>0.1\) |
-0.1 |
1 |
0 |
2 |
\(x_2>0.1\) |
-0.1 |
0 |
1 |
3 |
\(x_1+x_2<1\) |
1 |
-1 |
-1 |
4 |
\(x_1>0.25\) |
-0.25 |
1 |
0 |
5 |
\(x_2>0.25\) |
-0.25 |
0 |
1 |
6 |
\(x_1+x_2<0.8\) |
0.8 |
-1 |
-1 |
Warunki 1-3 zapewniają granice dla większego trójkąta, a 4-6 dla mniejszego, zawartego w większym. W drugiej warstwie neuronowej musimy zrealizować dwie bramki AND odpowiednio dla warunków 1-3 i 4-6, a zatem bierzemy
\(\alpha\) |
\(w_{0\alpha}^2\) |
\(w_{1\alpha}^2\) |
\(w_{2\alpha}^2\) |
\(w_{3\alpha}^2\) |
\(w_{4\alpha}^2\) |
\(w_{5\alpha}^2\) |
\(w_{6\alpha}^2\) |
|---|---|---|---|---|---|---|---|
1 |
-1 |
0.4 |
0.4 |
0.4 |
0 |
0 |
0 |
2 |
-1 |
0 |
0 |
0 |
0.4 |
0.4 |
0.4 |
Na koniec w warstwie wyjściowej realizujemy bramkę \(p \wedge \! \sim\! q\), skąd
\(\alpha\) |
\(w_{0\alpha}^3\) |
\(w_{1\alpha}^3\) |
\(w_{2\alpha}^3\) |
|---|---|---|---|
1 |
-1 |
1.2 |
-0.6 |
Łącząc to wszystko razem, uzyskujemy nastepujacy słownik wag:
w={1:np.array([[-0.1,-0.1,1,-0.25,-0.25,0.8],[1,0,-1,1,0,-1],[0,1,-1,0,1,-1]]),
2:np.array([[-1,-1],[0.4,0],[0.4,0],[0.4,0],[0,0.4],[0,0.4],[0,0.4]]),
3:np.array([[-1],[1.2],[-0.6]])}
Feed-forward dla prykładowego inputu daje
xi=[0.2,0.3]
x=func.feed_forward(arch,w,xi)
plt.show(draw.plot_net_w_x(arch,w,1,x))
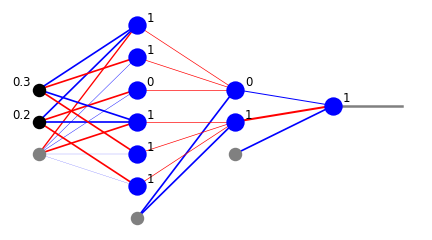
Właśnie odkryliśmy, że punkt [0.2,0.3] znajduje się w naszym obszarze (1 z warstwy wyjściowej). Właściwie mamy tutaj więcej informacji z warstw pośrednich. Z drugiej warstwy neuronowej widzimy, że punkt należy do większego trójkąta (1 z dolnego neuronu), a nie należy do mniejszego trójkąta (0 z górnego neuronu). Z pierwszej warstwy neuronowej możemy odczytać warunki z sześciu nierówności.
Następnie testujemy działanie naszej sieci dla innych punktów. Najpierw definiujemy funkcję generującą losowy punkt w kwadracie \([0,1]\times [0,1]\) i propagujemy go przez sieć. Przypisujemy mu etykietę 1, jeśli należy do żądanego obszaru, a 0 w przeciwnym razie. Następnie tworzymy dużą próbkę takich punktów i generujemy grafikę, używając koloru różowego dla etykiety 1 i niebieskiego dla etykiety 0.
def po():
xi=[np.random.random(),np.random.random()] # random point from the [0,1]x[0,1] square
x=func.feed_forward(arch,w,xi) # feed forward
return [xi[0],xi[1],x[3][0]] # the point's coordinates and label
samp=np.array([po() for _ in range(10000)])
print(samp[:5])
[[0.7088127 0.81098538 0. ]
[0.52044622 0.19265106 1. ]
[0.45637626 0.95670484 0. ]
[0.51723699 0.06066656 0. ]
[0.00879429 0.38239462 0. ]]
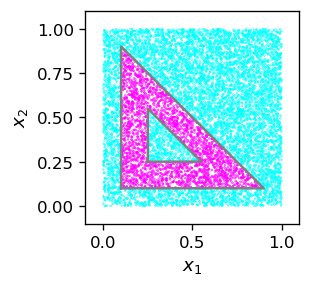
Widzimy, że nasza maszynka działa doskonale!
W tym miejscu czytelnik może słusznie powiedzieć, że powyższe wyniki są trywialne: w istocie właśnie zaimplementowaliśmy pewne warunki geometryczne i ich koniunkcje.
Jednak, podobnie jak w przypadku sieci jednowarstwowych, istnieje ważny argument przeciwko tej pozornej błahości. Wyobraźmy sobie ponownie, że mamy próbkę danych z etykietami i tylko tele, podobnie jak w przykładzie pojedynczego neuronu MCP z rozdziału Neuron MCP. Wtedy na początku nie mamy warunków granicznych i potrzebujemy jakiegoś skutecznego sposobu, aby je znaleźć. Właśnie to zadanie wykonuje za nas uczenie klasyfikatorów: ustala wagi w taki sposób, że odpowiednie warunki są domyślnie wbudowane. Po materiale z tego rozdziału czytelnik powinien być przekonany, że jest to jak najbardziej możliwe i nie ma w tym nic magicznego! W następnym rozdziale pokażemy, jak to praktycznie zrobić.
Ćwiczenia¶
\(~\)
Zaprojektuj sieć i uruchom kod z tego wykładu dla wybranego regionu wypukłego.
Zaprojektuj i zaprogramuj klasyfikator dla czterech kategorii punktów należących do regionów utworzonych przez dwie przecinające się linie (wskazówka: uwzględnij wiecej komórek wyjściowych).